Introduction

This guide will teach you the basics of using OpenGL to develop modern graphics applications. There are a lot of other guides on this topic, but there are some major points where this guide differs from those. We will not be discussing any of the old parts of the OpenGL specification. That means you'll be taught how to implement things yourself, instead of using deprecated functions like glBegin and glLight. Anything that is not directly related to OpenGL itself, like creating a window and loading textures from files, will be done using a few small libraries.

To show you how much it pays off to do things yourself, this guide also contains a lot of interactive examples to make it both fun and easy to learn all the different aspects of using a low-level graphics library like OpenGL!

As an added bonus, you always have the opportunity to ask questions at the end of each chapter in the comments section. I'll try to answer as many questions as possible, but always remember that there are plenty of people out there who are willing to help you with your issues. Make sure to help us help you by specifying your platform, compiler, the relevant code section, the result you expect and what is actually happening.

E-book

This guide is now available in e-book formats as well:

• EPUB
• PDF

Credits

Thanks to all of the contributors for their help with improving the quality of this tutorial! Special thanks to the following people for their essential contributions to the site:

• Toby Rufinus (code fixes, improved images, sample solutions for last chapters)
• Eric Engeström (making the site mobile friendly)
• Elliott Sales de Andrade (improving article text)
• Aaron Hamilton (improving article text)

Prerequisites

Before we can take off, you need to make sure you have all the things you need.

• A reasonable amount of experience with C++
• Graphics card compatible with OpenGL 3.2
• SFML, GLFW or SDL for creating the context and handling input
• GLEW to use newer OpenGL functions
• SOIL for textures
• GLM for vectors and matrices

Context creation will be explained for SFML, GLFW and SDL, so use whatever library suites you best. See the next chapter for the differences between the three if you're not sure which one to use.

You also have the option of creating the context yourself using Win32, Xlib or Cocoa, but your code will not be portable anymore. That means you can not use the same code for all platforms.

If you've got everything you need, let's begin.

Window and OpenGL context

Before you can start drawing things, you need to initialize OpenGL. This is done by creating an OpenGL context, which is essentially a state machine that stores all data related to the rendering of your application. When your application closes, the OpenGL context is destroyed and everything is cleaned up.

The problem is that creating a window and an OpenGL context is not part of the OpenGL specification. That means it is done differently on every platform out there! Developing applications using OpenGL is all about being portable, so this is the last thing we need. Luckily there are libraries out there that abstract this process, so that you can maintain the same codebase for all supported platforms.

While the available libraries out there all have advantages and disadvantages, they do all have a certain program flow in common. You start by specifying the properties of the game window, such as the title and the size and the properties of the OpenGL context, like the anti-aliasing level. Your application will then initiate the event loop, which contains an important set of tasks that need to be completed over and over again until the window closes. These tasks usually handle window events like mouse clicks, updating the rendering state and then drawing.

This program flow would look something like this in pseudocode:

#include <libraryheaders>

int main()
{
    createWindow(title, width, height);
    createOpenGLContext(settings);

    while (windowOpen)
    {
	while (event = newEvent())
		handleEvent(event);

	updateScene();

	drawGraphics();
	presentGraphics();
    }

    return 0;
}

When rendering a frame, the results will be stored in an offscreen buffer known as the back buffer to make sure the user only sees the final result. The presentGraphics() call will copy the result from the back buffer to the visible window buffer, the front buffer. Every application that makes use of real-time graphics will have a program flow that comes down to this, whether it uses a library or native code.

Supporting resizable windows with OpenGL introduces some complexities as resources need to be reloaded and buffers need to be recreated to fit the new window size. It's more convenient for the learning process to not bother with such details yet, so we'll only deal with fixed size (fullscreen) windows for now.

Setup

Instead of reading this chapter, you can make use of the OpenGL quickstart boilerplate, which makes setting up an OpenGL project with all of the required libraries very easy. You'll just have to install SOIL separately.

The first thing to do when starting a new OpenGL project is to dynamically link with OpenGL.

• Windows: Add opengl32.lib to your linker input
• Linux: Include -lGL in your compiler options
• OS X: Add -framework OpenGL to your compiler options

Make sure that you do not include opengl32.dll with your application. This file is already included with Windows and may differ per version, which will cause problems on other computers.

The rest of the steps depend on which library you choose to use for creating the window and context.

Libraries

There are many libraries around that can create a window and an accompanying OpenGL context for you. There is no best library out there, because everyone has different needs and ideals. I've chosen to discuss the process for the three most popular libraries here for completeness, but you can find more detailed guides on their respective websites. All code after this chapter will be independent of your choice of library here.

SFML

SFML is a cross-platform C++ multimedia library that provides access to graphics, input, audio, networking and the system. The downside of using this library is that it tries hard to be an all-in-one solution. You have little to no control over the creation of the OpenGL context, as it was designed to be used with its own set of drawing functions.

SDL

SDL is also a cross-platform multimedia library, but targeted at C. That makes it a bit rougher to use for C++ programmers, but it's an excellent alternative to SFML. It supports more exotic platforms and most importantly, offers more control over the creation of the OpenGL context than SFML.

GLFW

GLFW, as the name implies, is a C library specifically designed for use with OpenGL. Unlike SDL and SFML it only comes with the absolute necessities: window and context creation and input management. It offers the most control over the OpenGL context creation out of these three libraries.

Others

There are a few other options, like freeglut and OpenGLUT, but I personally think the aforementioned libraries are vastly superior in control, ease of use and on top of that more up-to-date.

SFML

The OpenGL context is created implicitly when opening a new window in SFML, so that's all you have to do. SFML also comes with a graphics package, but since we're going to use OpenGL directly, we don't need it.

Building

After you've downloaded the SFML binaries package or compiled it yourself, you'll find the needed files in the lib and include folders.

• Add the lib folder to your library path and link with sfml-system and sfml-window. With Visual Studio on Windows, link with the sfml-system-s and sfml-window-s files in lib/vc2008 instead.
• Add the include folder to your include path.

The SFML libraries have a simple naming convention for different configurations. If you want to dynamically link, simply remove the -s from the name, define SFML_DYNAMIC and copy the shared libraries. If you want to use the binaries with debug symbols, additionally append -d to the name.

To verify that you've done this correctly, try compiling and running the following code:

#include <SFML/System.hpp>

int main()
{
    sf::sleep(sf::seconds(1.f));
    return 0;
}

It should show a console application and exit after a second. If you run into any trouble, you can find more detailed information for Visual Studio, Code::Blocks and gcc in the tutorials on the SFML website.

Code

Start by including the window package and defining the entry point of your application.

#include <SFML/Window.hpp>

int main()
{
    return 0;
}

A window can be opened by creating a new instance of sf::Window. The basic constructor takes an sf::VideoMode structure, a title for the window and a window style. The sf::VideoMode structure specifies the width, height and optionally the pixel depth of the window. Finally, the requirement for a fixed size window is specified by overriding the default style of Style::Resize|Style::Close. It is also possible to create a fullscreen window by passing Style::Fullscreen as window style.

sf::ContextSettings settings;
settings.depthBits = 24;
settings.stencilBits = 8;
settings.antialiasingLevel = 2; // Optional
// Request OpenGL version 3.2
settings.majorVersion = 3;
settings.minorVersion = 2;
settings.attributeFlags = sf::ContextSettings::Core;

sf::Window window(sf::VideoMode(800, 600), "OpenGL", sf::Style::Close, settings);

The constructor can also take an sf::ContextSettings structure that allows you to request an OpenGL context and specify the anti-aliasing level and the accuracy of the depth and stencil buffers. The latter two will be discussed later, so you don't have to worry about these yet. In the latest version of SFML, you do need to request these manually with the code above. We request an OpenGL context of version 3.2 in the core profile as opposed to the compatibility mode which is default. Using the default compatibility mode may cause problems while using modern OpenGL on some systems, thus we use the core profile.

Note that these settings are only a hint, SFML will try to find the closest valid match. It will, for example, likely create a context with a newer OpenGL version than we specified.

When running this, you'll notice that the application instantly closes after creating the window. Let's add the event loop to deal with that.

bool running = true;
while (running)
{
    sf::Event windowEvent;
    while (window.pollEvent(windowEvent))
    {

    }
}

When something happens to your window, an event is posted to the event queue. There is a wide variety of events, including window size changes, mouse movement and key presses. It's up to you to decide which events require additional action, but there is at least one that needs to be handled to make your application run well.

switch (windowEvent.type)
{
case sf::Event::Closed:
    running = false;
    break;
}

When the user attempts to close the window, the Closed event is fired and we act on that by exiting the application. Try removing that line and you'll see that it's impossible to close the window by normal means. If you prefer a fullscreen window, you should add the escape key as a means to close the window:

case sf::Event::KeyPressed:
    if (windowEvent.key.code == sf::Keyboard::Escape)
   	running = false;
    break;

You have your window and the important events are acted upon, so you're now ready to put something on the screen. After drawing something, you can swap the back buffer and the front buffer with window.display().

When you run your application, you should see something like this:

Note that SFML allows you to have multiple windows. If you want to make use of this feature, make sure to call window.setActive() to activate a certain window for drawing operations.

Now that you have a window and a context, there's one more thing that needs to be done.

SDL

SDL comes with many different modules, but for creating a window with an accompanying OpenGL context we're only interested in the video module. It will take care of everything we need, so let's see how to use it.

Building

After you've downloaded the SDL binaries or compiled them yourself, you'll find the needed files in the lib and include folders.

• Add the lib folder to your library path and link with SDL2 and SDL2main.
• SDL uses dynamic linking, so make sure that the shared library (SDL2.dll, SDL2.so) is with your executable.
• Add the include folder to your include path.

To verify that you're ready, try compiling and running the following snippet of code:

#include <SDL.h>

int main(int argc, char *argv[])
{
    SDL_Init(SDL_INIT_EVERYTHING);

    SDL_Delay(1000);

    SDL_Quit();
    return 0;
}

It should show a console application and exit after a second. If you run into any trouble, you can find more detailed information for all kinds of platforms and compilers in the tutorials on the web.

Code

Start by defining the entry point of your application and include the headers for SDL.

#include <SDL.h>
#include <SDL_opengl.h>

int main(int argc, char *argv[])
{
    return 0;
}

To use SDL in an application, you need to tell SDL which modules you need and when to unload them. You can do this with two lines of code.

SDL_Init(SDL_INIT_VIDEO);
...
SDL_Quit();
return 0;

The SDL_Init function takes a bitfield with the modules to load. The video module includes everything you need to create a window and an OpenGL context.

Before doing anything else, first tell SDL that you want a forward compatible OpenGL 3.2 context:

SDL_GL_SetAttribute(SDL_GL_CONTEXT_PROFILE_MASK, SDL_GL_CONTEXT_PROFILE_CORE);
SDL_GL_SetAttribute(SDL_GL_CONTEXT_MAJOR_VERSION, 3);
SDL_GL_SetAttribute(SDL_GL_CONTEXT_MINOR_VERSION, 2);
SDL_GL_SetAttribute(SDL_GL_STENCIL_SIZE, 8);

You also need to tell SDL to create a stencil buffer, which will be relevant for a later chapter. After that, create a window using the SDL_CreateWindow function.

SDL_Window* window = SDL_CreateWindow("OpenGL", 100, 100, 800, 600, SDL_WINDOW_OPENGL);

The first argument specifies the title of the window, the next two are the X and Y position and the two after those are the width and height. If the position doesn't matter, you can specify SDL_WINDOWPOS_UNDEFINED or SDL_WINDOWPOS_CENTERED for the second and third argument. The final parameter specifies window properties like:

• SDL_WINDOW_OPENGL - Create a window ready for OpenGL.
• SDL_WINDOW_RESIZABLE - Create a resizable window.
• Optional SDL_WINDOW_FULLSCREEN - Create a fullscreen window.

After you've created the window, you can create the OpenGL context:

SDL_GLContext context = SDL_GL_CreateContext(window);
...
SDL_GL_DeleteContext(context);

The context should be destroyed right before calling SDL_Quit() to clean up the resources.

Then comes the most important part of the program, the event loop:

SDL_Event windowEvent;
while (true)
{
    if (SDL_PollEvent(&windowEvent))
    {
	if (windowEvent.type == SDL_QUIT) break;
    }

    SDL_GL_SwapWindow(window);
}

The SDL_PollEvent function will check if there are any new events that have to be handled. An event can be anything from a mouse click to the user moving the window. Right now, the only event you need to respond to is the user pressing the little X button in the corner of the window. By breaking from the main loop, SDL_Quit is called and the window and graphics surface are destroyed. SDL_GL_SwapWindow here takes care of swapping the front and back buffer after new things have been drawn by your application.

If you have a fullscreen window, it would be preferable to use the escape key as a means to close the window.

if (windowEvent.type == SDL_KEYUP &&
    windowEvent.key.keysym.sym == SDLK_ESCAPE) break;

When you run your application now, you should see something like this:

Now that you have a window and a context, there's one more thing that needs to be done.

GLFW

GLFW is tailored specifically for using OpenGL, so it is by far the easiest to use for our purpose.

Building

After you've downloaded the GLFW binaries package from the website or compiled the library yourself, you'll find the headers in the include folder and the libraries for your compiler in one of the lib folders.

• Add the appropriate lib folder to your library path and link with GLFW.
• Add the include folder to your include path.

You can also dynamically link with GLFW if you want to. Simply link with GLFWDLL and include the shared library with your executable.

Here is a simple snippet of code to check your build configuration:

#include <GLFW/glfw3.h>
#include <thread>

int main()
{
    glfwInit();
    std::this_thread::sleep_for(std::chrono::seconds(1));
    glfwTerminate();
}

It should show a console application and exit after a second. If you run into any trouble, just ask in the comments and you'll receive help.

Code

Start by simply including the GLFW header and define the entry point of the application.

#include <GLFW/glfw3.h>

int main()
{
    return 0;
}

To use GLFW, it needs to be initialised when the program starts and you need to give it a chance to clean up when your program closes. The glfwInit and glfwTerminate functions are geared towards that purpose.

glfwInit();
...
glfwTerminate();

The next thing to do is creating and configuring the window. Before calling glfwCreateWindow, we first set some options.

glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 2);
glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);

glfwWindowHint(GLFW_RESIZABLE, GL_FALSE);

GLFWwindow* window = glfwCreateWindow(800, 600, "OpenGL", nullptr, nullptr); // Windowed
GLFWwindow* window =
    glfwCreateWindow(800, 600, "OpenGL", glfwGetPrimaryMonitor(), nullptr); // Fullscreen

You'll immediately notice the first three lines of code that are only relevant for this library. It is specified that we require the OpenGL context to support OpenGL 3.2 at the least. The GLFW_OPENGL_PROFILE option specifies that we want a context that only supports the new core functionality.

The first two parameters of glfwCreateWindow specify the width and height of the drawing surface and the third parameter specifies the window title. The fourth parameter should be set to NULL for windowed mode and glfwGetPrimaryMonitor() for fullscreen mode. The last parameter allows you to specify an existing OpenGL context to share resources like textures with. The glfwWindowHint function is used to specify additional requirements for a window.

After creating the window, the OpenGL context has to be made active:

glfwMakeContextCurrent(window);

Next comes the event loop, which in the case of GLFW works a little differently than the other libraries. GLFW uses a so-called closed event loop, which means you only have to handle events when you need to. That means your event loop will look really simple:

while(!glfwWindowShouldClose(window))
{
    glfwSwapBuffers(window);
    glfwPollEvents();
}

The only required functions in the loop are glfwSwapBuffers to swap the back buffer and front buffer after you've finished drawing and glfwPollEvents to retrieve window events. If you are making a fullscreen application, you should handle the escape key to easily return to the desktop.

if (glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS)
	glfwSetWindowShouldClose(window, GL_TRUE);

If you want to learn more about handling input, you can refer to the documentation.

You should now have a window or a full screen surface with an OpenGL context. Before you can start drawing stuff however, there's one more thing that needs to be done.

One more thing

Unfortunately, we can't just call the functions we need yet. This is because it's the duty of the graphics card vendor to implement OpenGL functionality in their drivers based on what the graphics card supports. You wouldn't want your program to only be compatible with a single driver version and graphics card, so we'll have to do something clever.

Your program needs to check which functions are available at runtime and link with them dynamically. This is done by finding the addresses of the functions, assigning them to function pointers and calling them. That looks something like this:

Don't try to run this code, it's just for demonstration purposes.

// Specify prototype of function
typedef void (*GENBUFFERS) (GLsizei, GLuint*);

// Load address of function and assign it to a function pointer
GENBUFFERS glGenBuffers = (GENBUFFERS)wglGetProcAddress("glGenBuffers");
// or Linux:
GENBUFFERS glGenBuffers = (GENBUFFERS)glXGetProcAddress((const GLubyte *) "glGenBuffers");
// or OSX:
GENBUFFERS glGenBuffers = (GENBUFFERS)NSGLGetProcAddress("glGenBuffers");

// Call function as normal
GLuint buffer;
glGenBuffers(1, &buffer);

Let me begin by asserting that it is perfectly normal to be scared by this snippet of code. You may not be familiar with the concept of function pointers yet, but at least try to roughly understand what is happening here. You can imagine that going through this process of defining prototypes and finding addresses of functions is very tedious and in the end nothing more than a complete waste of time.

The good news is that there are libraries that have solved this problem for us. The most popular and best maintained library right now is GLEW and there's no reason for that to change anytime soon. Nevertheless, the alternative library GLEE works almost completely the same save for the initialization and cleanup code.

If you haven't built GLEW yet, do so now. We'll now add GLEW to your project.

• Start by linking your project with the static GLEW library in the lib folder. This is either glew32s.lib or GLEW depending on your platform.
• Add the include folder to your include path.

Now just include the header in your program, but make sure that it is included before the OpenGL headers or the library you used to create your window.

#define GLEW_STATIC
#include <GL/glew.h>

Don't forget to define GLEW_STATIC either using this preprocessor directive or by adding the -DGLEW_STATIC directive to your compiler command-line parameters or project settings.

If you prefer to dynamically link with GLEW, leave out the define and link with glew32.lib instead of glew32s.lib on Windows. Don't forget to include glew32.dll or libGLEW.so with your executable!

Now all that's left is calling glewInit() after the creation of your window and OpenGL context. The glewExperimental line is necessary to force GLEW to use a modern OpenGL method for checking if a function is available.

glewExperimental = GL_TRUE;
glewInit();

Make sure that you've set up your project correctly by calling the glGenBuffers function, which was loaded by GLEW for you!

GLuint vertexBuffer;
glGenBuffers(1, &vertexBuffer);

printf("%u\n", vertexBuffer);

Your program should compile and run without issues and display the number 1 in your console. If you need more help with using GLEW, you can refer to the website or ask in the comments.

Now that we're past all of the configuration and initialization work, I'd advise you to make a copy of your current project so that you won't have to write all of the boilerplate code again when starting a new project.

Now, let's get to drawing things!

The graphics pipeline

By learning OpenGL, you've decided that you want to do all of the hard work yourself. That inevitably means that you'll be thrown in the deep, but once you understand the essentials, you'll see that doing things the hard way doesn't have to be so difficult after all. To top that all, the exercises at the end of this chapter will show you the sheer amount of control you have over the rendering process by doing things the modern way!

The graphics pipeline covers all of the steps that follow each other up on processing the input data to get to the final output image. I'll explain these steps with help of the following illustration.

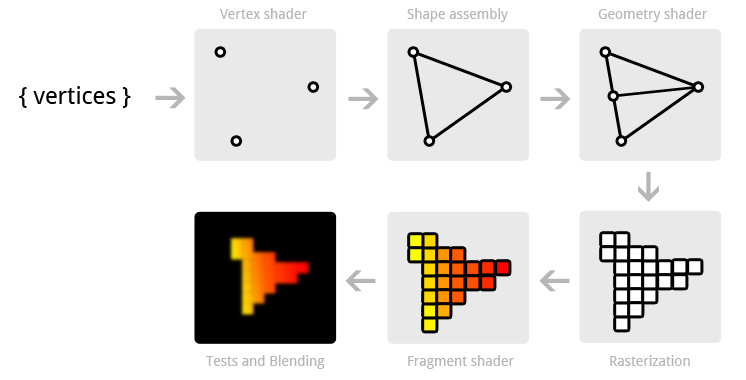
It all begins with the vertices, these are the points from which shapes like triangles will later be constructed. Each of these points is stored with certain attributes and it's up to you to decide what kind of attributes you want to store. Commonly used attributes are 3D position in the world and texture coordinates.

The vertex shader is a small program running on your graphics card that processes every one of these input vertices individually. This is where the perspective transformation takes place, which projects vertices with a 3D world position onto your 2D screen! It also passes important attributes like color and texture coordinates further down the pipeline.

After the input vertices have been transformed, the graphics card will form triangles, lines or points out of them. These shapes are called primitives because they form the basis of more complex shapes. There are some additional drawing modes to choose from, like triangle strips and line strips. These reduce the number of vertices you need to pass if you want to create objects where each next primitive is connected to the last one, like a continuous line consisting of several segments.

The following step, the geometry shader, is completely optional and was only recently introduced. Unlike the vertex shader, the geometry shader can output more data than comes in. It takes the primitives from the shape assembly stage as input and can either pass a primitive through down to the rest of the pipeline, modify it first, completely discard it or even replace it with other primitive(s). Since the communication between the GPU and the rest of the PC is relatively slow, this stage can help you reduce the amount of data that needs to be transferred. With a voxel game for example, you could pass vertices as point vertices, along with an attribute for their world position, color and material and the actual cubes can be produced in the geometry shader with a point as input!

After the final list of shapes is composed and converted to screen coordinates, the rasterizer turns the visible parts of the shapes into pixel-sized fragments. The vertex attributes coming from the vertex shader or geometry shader are interpolated and passed as input to the fragment shader for each fragment. As you can see in the image, the colors are smoothly interpolated over the fragments that make up the triangle, even though only 3 points were specified.

The fragment shader processes each individual fragment along with its interpolated attributes and should output the final color. This is usually done by sampling from a texture using the interpolated texture coordinate vertex attributes or simply outputting a color. In more advanced scenarios, there could also be calculations related to lighting and shadowing and special effects in this program. The shader also has the ability to discard certain fragments, which means that a shape will be see-through there.

Finally, the end result is composed from all these shape fragments by blending them together and performing depth and stencil testing. All you need to know about these last two right now, is that they allow you to use additional rules to throw away certain fragments and let others pass. For example, if one triangle is obscured by another triangle, the fragment of the closer triangle should end up on the screen.

Now that you know how your graphics card turns an array of vertices into an image on the screen, let's get to work!

Vertex input

The first thing you have to decide on is what data the graphics card is going to need to draw your scene correctly. As mentioned above, this data comes in the form of vertex attributes. You're free to come up with any kind of attribute you want, but it all inevitably begins with the world position. Whether you're doing 2D graphics or 3D graphics, this is the attribute that will determine where the objects and shapes end up on your screen in the end.

Device coordinates

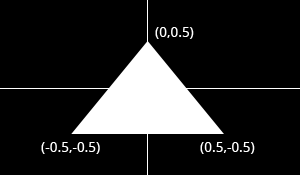
When your vertices have been processed by the pipeline outlined above, their coordinates will have been transformed into device coordinates. Device X and Y coordinates are mapped to the screen between -1 and 1.

Just like a graph, the center has coordinates (0,0) and the y axis is positive above the center. This seems unnatural because graphics applications usually have (0,0) in the top-left corner and (width,height) in the bottom-right corner, but it's an excellent way to simplify 3D calculations and to stay resolution independent.

The triangle above consists of 3 vertices positioned at (0,0.5), (0.5,-0.5) and (-0.5,-0.5) in clockwise order. It is clear that the only variation between the vertices here is the position, so that's the only attribute we need. Since we're passing the device coordinates directly, an X and Y coordinate suffices for the position.

OpenGL expects you to send all of your vertices in a single array, which may be confusing at first. To understand the format of this array, let's see what it would look like for our triangle.

float vertices[] = {
	 0.0f,  0.5f, // Vertex 1 (X, Y)
	 0.5f, -0.5f, // Vertex 2 (X, Y)
	-0.5f, -0.5f  // Vertex 3 (X, Y)
};

As you can see, this array should simply be a list of all vertices with their attributes packed together. The order in which the attributes appear doesn't matter, as long as it's the same for each vertex. The order of the vertices doesn't have to be sequential (i.e. the order in which shapes are formed), but this requires us to provide extra data in the form of an element buffer. This will be discussed at the end of this chapter as it would just complicate things for now.

The next step is to upload this vertex data to the graphics card. This is important because the memory on your graphics card is much faster and you won't have to send the data again every time your scene needs to be rendered (about 60 times per second).

This is done by creating a Vertex Buffer Object (VBO):

GLuint vbo;
glGenBuffers(1, &vbo); // Generate 1 buffer

The memory is managed by OpenGL, so instead of a pointer you get a positive number as a reference to it. GLuint is simply a cross-platform substitute for unsigned int, just like GLint is one for int. You will need this number to make the VBO active and to destroy it when you're done with it.

To upload the actual data to it you first have to make it the active object by calling glBindBuffer:

glBindBuffer(GL_ARRAY_BUFFER, vbo);

As hinted by the GL_ARRAY_BUFFER enum value there are other types of buffers, but they are not important right now. This statement makes the VBO we just created the active array buffer. Now that it's active we can copy the vertex data to it.

glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

Notice that this function doesn't refer to the id of our VBO, but instead to the active array buffer. The second parameter specifies the size in bytes. The final parameter is very important and its value depends on the usage of the vertex data. I'll outline the ones related to drawing here:

• GL_STATIC_DRAW: The vertex data will be uploaded once and drawn many times (e.g. the world).
• GL_DYNAMIC_DRAW: The vertex data will be created once, changed from time to time, but drawn many times more than that.
• GL_STREAM_DRAW: The vertex data will be uploaded once and drawn once.

This usage value will determine in what kind of memory the data is stored on your graphics card for the highest efficiency. For example, VBOs with GL_STREAM_DRAW as type may store their data in memory that allows faster writing in favour of slightly slower drawing.

The vertices with their attributes have been copied to the graphics card now, but they're not quite ready to be used yet. Remember that we can make up any kind of attribute we want and in any order, so now comes the moment where you have to explain to the graphics card how to handle these attributes. This is where you'll see how flexible modern OpenGL really is.

Shaders

As discussed earlier, there are three shader stages your vertex data will pass through. Each shader stage has a strictly defined purpose and in older versions of OpenGL, you could only slightly tweak what happened and how it happened. With modern OpenGL, it's up to us to instruct the graphics card what to do with the data. This is why it's possible to decide per application what attributes each vertex should have. You'll have to implement both the vertex and fragment shader to get something on the screen, the geometry shader is optional and is discussed later.

Shaders are written in a C-style language called GLSL (OpenGL Shading Language). OpenGL will compile your program from source at runtime and copy it to the graphics card. Each version of OpenGL has its own version of the shader language with availability of a certain feature set and we will be using GLSL 1.50. This version number may seem a bit off when we're using OpenGL 3.2, but that's because shaders were only introduced in OpenGL 2.0 as GLSL 1.10. Starting from OpenGL 3.3, this problem was solved and the GLSL version is the same as the OpenGL version.

Vertex shader

The vertex shader is a program on the graphics card that processes each vertex and its attributes as they appear in the vertex array. Its duty is to output the final vertex position in device coordinates and to output any data the fragment shader requires. That's why the 3D transformation should take place here. The fragment shader depends on attributes like the color and texture coordinates, which will usually be passed from input to output without any calculations.

Remember that our vertex position is already specified as device coordinates and no other attributes exist, so the vertex shader will be fairly bare bones.

#version 150 core

in vec2 position;

void main()
{
    gl_Position = vec4(position, 0.0, 1.0);
}

The #version preprocessor directive is used to indicate that the code that follows is GLSL 1.50 code using OpenGL's core profile. Next, we specify that there is only one attribute, the position. Apart from the regular C types, GLSL has built-in vector and matrix types identified by vec* and mat* identifiers. The type of the values within these constructs is always a float. The number after vec specifies the number of components (x, y, z, w) and the number after mat specifies the number of rows /columns. Since the position attribute consists of only an X and Y coordinate, vec2 is perfect.

You can be quite creative when working with these vertex types. In the example above a shortcut was used to set the first two components of the vec4 to those of vec2. These two lines are equal:

gl_Position = vec4(position, 0.0, 1.0);
gl_Position = vec4(position.x, position.y, 0.0, 1.0);

When you're working with colors, you can also access the individual components with r, g, b and a instead of x, y, z and w. This makes no difference and can help with clarity.

The final position of the vertex is assigned to the special gl_Position variable, because the position is needed for primitive assembly and many other built-in processes. For these to function correctly, the last value w needs to have a value of 1.0f. Other than that, you're free to do anything you want with the attributes and we'll see how to output those when we add color to the triangle later in this chapter.

Fragment shader

The output from the vertex shader is interpolated over all the pixels on the screen covered by a primitive. These pixels are called fragments and this is what the fragment shader operates on. Just like the vertex shader it has one mandatory output, the final color of a fragment. It's up to you to write the code for computing this color from vertex colors, texture coordinates and any other data coming from the vertex shader.

Our triangle only consists of white pixels, so the fragment shader simply outputs that color every time:

#version 150 core

out vec4 outColor;

void main()
{
    outColor = vec4(1.0, 1.0, 1.0, 1.0);
}

You'll immediately notice that we're not using some built-in variable for outputting the color, say gl_FragColor. This is because a fragment shader can in fact output multiple colors and we'll see how to handle this when actually loading these shaders. The outColor variable uses the type vec4, because each color consists of a red, green, blue and alpha component. Colors in OpenGL are generally represented as floating point numbers between 0.0 and 1.0 instead of the common 0 and 255.

Compiling shaders

Compiling shaders is easy once you have loaded the source code (either from file or as a hard-coded string). You can easily include your shader source in the C++ code through C++11 raw string literals:

const char* vertexSource = R"glsl(
    #version 150 core

    in vec2 position;

    void main()
    {
       gl_Position = vec4(position, 0.0, 1.0);
    }
)glsl";

Just like vertex buffers, creating a shader itself starts with creating a shader object and loading data into it.

GLuint vertexShader = glCreateShader(GL_VERTEX_SHADER);
glShaderSource(vertexShader, 1, &vertexSource, NULL);

Unlike VBOs, you can simply pass a reference to shader functions instead of making it active or anything like that. The glShaderSource function can take multiple source strings in an array, but you'll usually have your source code in one char array. The last parameter can contain an array of source code string lengths, passing NULL simply makes it stop at the null terminator.

All that's left is compiling the shader into code that can be executed by the graphics card now:

glCompileShader(vertexShader);

Be aware that if the shader fails to compile, e.g. because of a syntax error, glGetError will not report an error! See the block below for info on how to debug shaders.

Checking if a shader compiled successfully

GLint status;
glGetShaderiv(vertexShader, GL_COMPILE_STATUS, &status);

If status is equal to GL_TRUE, then your shader was compiled successfully.

> Retrieving the compile log

char buffer[512];
glGetShaderInfoLog(vertexShader, 512, NULL, buffer);

This will store the first 511 bytes + null terminator of the compile log in the specified buffer. The log may also report useful warnings even when compiling was successful, so it's useful to check it out from time to time when you develop your shaders.

The fragment shader is compiled in exactly the same way:

GLuint fragmentShader = glCreateShader(GL_FRAGMENT_SHADER);
glShaderSource(fragmentShader, 1, &fragmentSource, NULL);
glCompileShader(fragmentShader);

Again, be sure to check if your shader was compiled successfully, because it will save you from a headache later on.

Combining shaders into a program

Up until now the vertex and fragment shaders have been two separate objects. While they've been programmed to work together, they aren't actually connected yet. This connection is made by creating a program out of these two shaders.

GLuint shaderProgram = glCreateProgram();
glAttachShader(shaderProgram, vertexShader);
glAttachShader(shaderProgram, fragmentShader);

Since a fragment shader is allowed to write to multiple framebuffers, you need to explicitly specify which output is written to which framebuffer. This needs to happen before linking the program. However, since this is 0 by default and there's only one output right now, the following line of code is not necessary:

glBindFragDataLocation(shaderProgram, 0, "outColor");

Use glDrawBuffers when rendering to multiple framebuffers, because only the first output will be enabled by default.

After attaching both the fragment and vertex shaders, the connection is made by linking the program. It is allowed to make changes to the shaders after they've been added to a program (or multiple programs!), but the actual result will not change until a program has been linked again. It is also possible to attach multiple shaders for the same stage (e.g. fragment) if they're parts forming the whole shader together. A shader object can be deleted with glDeleteShader, but it will not actually be removed before it has been detached from all programs with glDetachShader.

glLinkProgram(shaderProgram);

To actually start using the shaders in the program, you just have to call:

glUseProgram(shaderProgram);

Just like a vertex buffer, only one program can be active at a time.

Making the link between vertex data and attributes

Although we have our vertex data and shaders now, OpenGL still doesn't know how the attributes are formatted and ordered. You first need to retrieve a reference to the position input in the vertex shader:

GLint posAttrib = glGetAttribLocation(shaderProgram, "position");

The location is a number depending on the order of the input definitions. The first and only input position in this example will always have location 0.

With the reference to the input, you can specify how the data for that input is retrieved from the array:

glVertexAttribPointer(posAttrib, 2, GL_FLOAT, GL_FALSE, 0, 0);

The first parameter references the input. The second parameter specifies the number of values for that input, which is the same as the number of components of the vec. The third parameter specifies the type of each component and the fourth parameter specifies whether the input values should be normalized between -1.0 and 1.0 (or 0.0 and 1.0 depending on the format) if they aren't floating point numbers.

The last two parameters are arguably the most important here as they specify how the attribute is laid out in the vertex array. The first number specifies the stride, or how many bytes are between each position attribute in the array. The value 0 means that there is no data in between. This is currently the case as the position of each vertex is immediately followed by the position of the next vertex. The last parameter specifies the offset, or how many bytes from the start of the array the attribute occurs. Since there are no other attributes, this is 0 as well.

It is important to know that this function will store not only the stride and the offset, but also the VBO that is currently bound to GL_ARRAY_BUFFER. That means that you don't have to explicitly bind the correct VBO when the actual drawing functions are called. This also implies that you can use a different VBO for each attribute.

Don't worry if you don't fully understand this yet, as we'll see how to alter this to add more attributes soon enough.

glEnableVertexAttribArray(posAttrib);

Last, but not least, the vertex attribute array needs to be enabled.

Vertex Array Objects

You can imagine that real graphics programs use many different shaders and vertex layouts to take care of a wide variety of needs and special effects. Changing the active shader program is easy enough with a call to glUseProgram, but it would be quite inconvenient if you had to set up all of the attributes again every time.

Luckily, OpenGL solves that problem with Vertex Array Objects (VAO). VAOs store all of the links between the attributes and your VBOs with raw vertex data.

A VAO is created in the same way as a VBO:

GLuint vao;
glGenVertexArrays(1, &vao);

To start using it, simply bind it:

glBindVertexArray(vao);

As soon as you've bound a certain VAO, every time you call glVertexAttribPointer, that information will be stored in that VAO. This makes switching between different vertex data and vertex formats as easy as binding a different VAO! Just remember that a VAO doesn't store any vertex data by itself, it just references the VBOs you've created and how to retrieve the attribute values from them.

Since only calls after binding a VAO stick to it, make sure that you've created and bound the VAO at the start of your program. Any vertex buffers and element buffers bound before it will be ignored.

Drawing

Now that you've loaded the vertex data, created the shader programs and linked the data to the attributes, you're ready to draw the triangle. The VAO that was used to store the attribute information is already bound, so you don't have to worry about that. All that's left is to simply call glDrawArrays in your main loop:

glDrawArrays(GL_TRIANGLES, 0, 3);

The first parameter specifies the kind of primitive (commonly point, line or triangle), the second parameter specifies how many vertices to skip at the beginning and the last parameter specifies the number of vertices (not primitives!) to process.

When you run your program now, you should see the following:

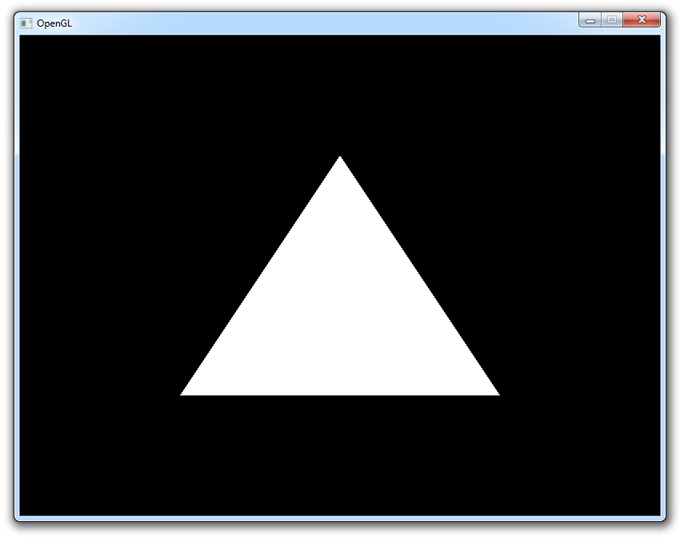
If you don't see anything, make sure that the shaders have compiled correctly, that the program has linked correctly, that the attribute array has been enabled, that the VAO has been bound before specifying the attributes, that your vertex data is correct and that glGetError returns 0. If you can't find the problem, try comparing your code to this sample.

Uniforms

Right now the white color of the triangle has been hard-coded into the shader code, but what if you wanted to change it after compiling the shader? As it turns out, vertex attributes are not the only way to pass data to shader programs. There is another way to pass data to the shaders called uniforms. These are essentially global variables, having the same value for all vertices and/or fragments. To demonstrate how to use these, let's make it possible to change the color of the triangle from the program itself.

By making the color in the fragment shader a uniform, it will end up looking like this:

#version 150 core

uniform vec3 triangleColor;

out vec4 outColor;

void main()
{
    outColor = vec4(triangleColor, 1.0);
}

The last component of the output color is transparency, which is not very interesting right now. If you run your program now you'll see that the triangle is black, because the value of triangleColor hasn't been set yet.

Changing the value of a uniform is just like setting vertex attributes, you first have to grab the location:

GLint uniColor = glGetUniformLocation(shaderProgram, "triangleColor");

The values of uniforms are changed with any of the glUniformXY functions, where X is the number of components and Y is the type. Common types are f (float), d (double) and i (integer).

glUniform3f(uniColor, 1.0f, 0.0f, 0.0f);

If you run your program now, you'll see that the triangle is red. To make things a little more exciting, try varying the color with the time by doing something like this in your main loop:

auto t_start = std::chrono::high_resolution_clock::now();

...

auto t_now = std::chrono::high_resolution_clock::now();
float time = std::chrono::duration_cast<std::chrono::duration<float>>(t_now - t_start).count();

glUniform3f(uniColor, (sin(time * 4.0f) + 1.0f) / 2.0f, 0.0f, 0.0f);

Although this example may not be very exciting, it does demonstrate that uniforms are essential for controlling the behaviour of shaders at runtime. Vertex attributes on the other hand are ideal for describing a single vertex.

See the code if you have any trouble getting this to work.

Adding some more colors

Although uniforms have their place, color is something we'd rather like to specify per corner of the triangle! Let's add a color attribute to the vertices to accomplish this.

We'll first have to add the extra attributes to the vertex data. Transparency isn't really relevant, so we'll only add the red, green and blue components:

float vertices[] = {
     0.0f,  0.5f, 1.0f, 0.0f, 0.0f, // Vertex 1: Red
     0.5f, -0.5f, 0.0f, 1.0f, 0.0f, // Vertex 2: Green
    -0.5f, -0.5f, 0.0f, 0.0f, 1.0f  // Vertex 3: Blue
};

Then we have to change the vertex shader to take it as input and pass it to the fragment shader:

#version 150 core

in vec2 position;
in vec3 color;

out vec3 Color;

void main()
{
    Color = color;
    gl_Position = vec4(position, 0.0, 1.0);
}

And Color is added as input to the fragment shader:

#version 150 core

in vec3 Color;

out vec4 outColor;

void main()
{
    outColor = vec4(Color, 1.0);
}

Make sure that the output of the vertex shader and the input of the fragment shader have the same name, or the shaders will not be linked properly.

Now, we just need to alter the attribute pointer code a bit to accommodate for the new X, Y, R, G, B attribute order.

GLint posAttrib = glGetAttribLocation(shaderProgram, "position");
glEnableVertexAttribArray(posAttrib);
glVertexAttribPointer(posAttrib, 2, GL_FLOAT, GL_FALSE,
    					   5*sizeof(float), 0);

    GLint colAttrib = glGetAttribLocation(shaderProgram, "color");
    glEnableVertexAttribArray(colAttrib);
    glVertexAttribPointer(colAttrib, 3, GL_FLOAT, GL_FALSE,
    					   5*sizeof(float), (void*)(2*sizeof(float)));

The fifth parameter is set to 5*sizeof(float) now, because each vertex consists of 5 floating point attribute values. The offset of 2*sizeof(float) for the color attribute is there because each vertex starts with 2 floating point values for the position that it has to skip over.

And we're done!

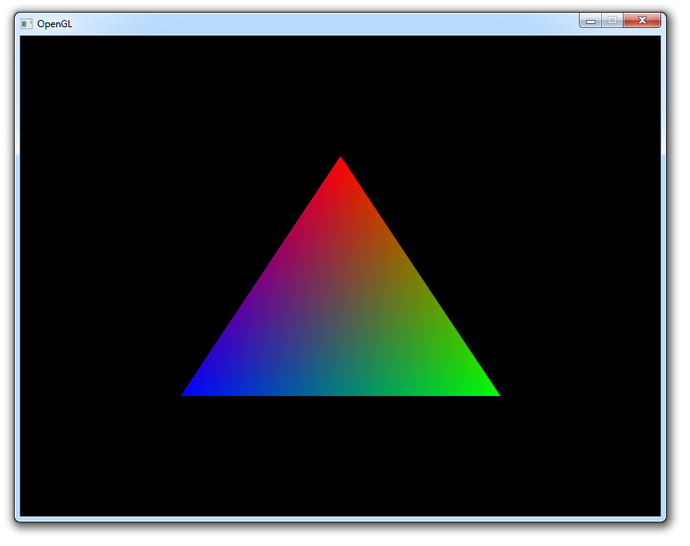
You should now have a reasonable understanding of vertex attributes and shaders. If you ran into problems, ask in the comments or have a look at the altered source code.

Element buffers

Right now, the vertices are specified in the order in which they are drawn. If you wanted to add another triangle, you would have to add 3 additional vertices to the vertex array. There is a way to control the order, which also enables you to reuse existing vertices. This can save you a lot of memory when working with real 3D models later on, because each point is usually occupied by a corner of three triangles!

An element array is filled with unsigned integers referring to vertices bound to GL_ARRAY_BUFFER. If we just want to draw them in the order they are in now, it'll look like this:

GLuint elements[] = {
    0, 1, 2
};

They are loaded into video memory through a VBO just like the vertex data:

GLuint ebo;
glGenBuffers(1, &ebo);

...

glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, ebo);
glBufferData(GL_ELEMENT_ARRAY_BUFFER,
    sizeof(elements), elements, GL_STATIC_DRAW);

The only thing that differs is the target, which is GL_ELEMENT_ARRAY_BUFFER this time.

To actually make use of this buffer, you'll have to change the draw command:

glDrawElements(GL_TRIANGLES, 3, GL_UNSIGNED_INT, 0);

The first parameter is the same as with glDrawArrays, but the other ones all refer to the element buffer. The second parameter specifies the number of indices to draw, the third parameter specifies the type of the element data and the last parameter specifies the offset. The only real difference is that you're talking about indices instead of vertices now.

To see how an element buffer can be beneficial, let's try drawing a rectangle using two triangles. We'll start by doing it without an element buffer.

float vertices[] = {
    -0.5f,  0.5f, 1.0f, 0.0f, 0.0f, // Top-left
     0.5f,  0.5f, 0.0f, 1.0f, 0.0f, // Top-right
     0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // Bottom-right

     0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // Bottom-right
    -0.5f, -0.5f, 1.0f, 1.0f, 1.0f, // Bottom-left
    -0.5f,  0.5f, 1.0f, 0.0f, 0.0f  // Top-left
};

By calling glDrawArrays instead of glDrawElements like before, the element buffer will simply be ignored:

glDrawArrays(GL_TRIANGLES, 0, 6);

The rectangle is rendered as it should, but the repetition of vertex data is a waste of memory. Using an element buffer allows you to reuse data:

float vertices[] = {
    -0.5f,  0.5f, 1.0f, 0.0f, 0.0f, // Top-left
     0.5f,  0.5f, 0.0f, 1.0f, 0.0f, // Top-right
     0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // Bottom-right
    -0.5f, -0.5f, 1.0f, 1.0f, 1.0f  // Bottom-left
};

...

GLuint elements[] = {
    0, 1, 2,
    2, 3, 0
};

...

glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);

The element buffer still specifies 6 vertices to form 2 triangles like before, but now we're able to reuse vertices! This may not seem like much of a big deal at this point, but when your graphics application loads many models into the relatively small graphics memory, element buffers will be an important area of optimization.

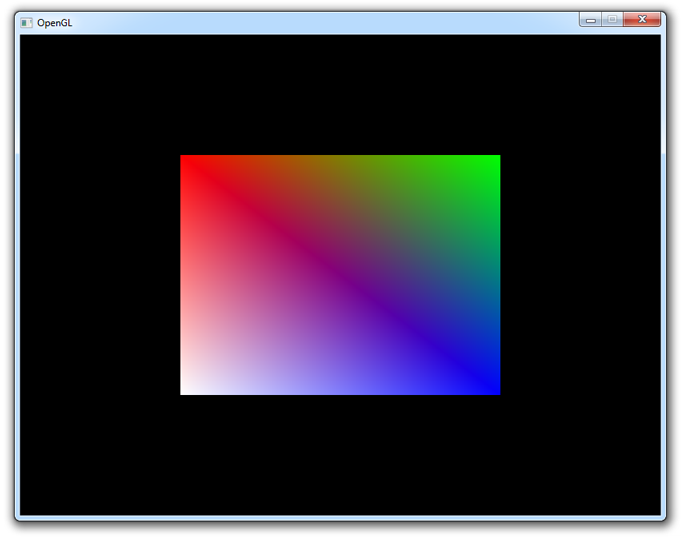
If you run into trouble, have a look at the full source code.

This chapter has covered all of the core principles of drawing things with OpenGL and it's absolutely essential that you have a good understanding of them before continuing. Therefore I advise you to do the exercises below before diving into textures.

Exercises

• Alter the vertex shader so that the triangle is upside down. (Solution)
• Invert the colors of the triangle by altering the fragment shader. (Solution)
• Change the program so that each vertex has only one color value, determining the shade of gray. (Solution)

Textures objects and parameters

Just like VBOs and VAOs, textures are objects that need to be generated first by calling a function. It shouldn't be a surprise at this point what this function is called.

GLuint tex;
glGenTextures(1, &tex);

Textures are typically used for images to decorate 3D models, but in reality they can be used to store many different kinds of data. It's possible to have 1D, 2D and even 3D textures, which can be used to store bulk data on the GPU. An example of another use for textures is storing terrain information. This article will pay attention to the use of textures for images, but the principles generally apply to all kinds of textures.

glBindTexture(GL_TEXTURE_2D, tex);

Just like other objects, textures have to be bound to apply operations to them. Since images are 2D arrays of pixels, it will be bound to the GL_TEXTURE_2D target.

The pixels in the texture will be addressed using texture coordinates during drawing operations. These coordinates range from 0.0 to 1.0 where (0,0) is conventionally the bottom-left corner and (1,1) is the top-right corner of the texture image. The operation that uses these texture coordinates to retrieve color information from the pixels is called sampling. There are different ways to approach this problem, each being appropriate for different scenarios. OpenGL offers you many options to control how this sampling is done, of which the common ones will be discussed here.

Wrapping

The first thing you'll have to consider is how the texture should be sampled when a coordinate outside the range of 0 to 1 is given. OpenGL offers 4 ways of handling this:

• GL_REPEAT: The integer part of the coordinate will be ignored and a repeating pattern is formed.
• GL_MIRRORED_REPEAT: The texture will also be repeated, but it will be mirrored when the integer part of the coordinate is odd.
• GL_CLAMP_TO_EDGE: The coordinate will simply be clamped between 0 and 1.
• GL_CLAMP_TO_BORDER: The coordinates that fall outside the range will be given a specified border color.

These explanations may still be a bit cryptic and since OpenGL is all about graphics, let's see what all of these cases actually look like:

The wrapping can be set per coordinate, where the equivalent of (x,y,z) in texture coordinates is called (s,t,r). Texture parameter are changed with the glTexParameter* functions as demonstrated here.

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);

As before, the i here indicates the type of the value you want to specify. If you use GL_CLAMP_TO_BORDER and you want to change the border color, you need to change the value of GL_TEXTURE_BORDER_COLOR by passing an RGBA float array:

float color[] = { 1.0f, 0.0f, 0.0f, 1.0f };
glTexParameterfv(GL_TEXTURE_2D, GL_TEXTURE_BORDER_COLOR, color);

This operation will set the border color to red.

Filtering

Since texture coordinates are resolution independent, they won't always match a pixel exactly. This happens when a texture image is stretched beyond its original size or when it's sized down. OpenGL offers various methods to decide on the sampled color when this happens. This process is called filtering and the following methods are available:

• GL_NEAREST: Returns the pixel that is closest to the coordinates.
• GL_LINEAR: Returns the weighted average of the 4 pixels surrounding the given coordinates.
• GL_NEAREST_MIPMAP_NEAREST, GL_LINEAR_MIPMAP_NEAREST, GL_NEAREST_MIPMAP_LINEAR, GL_LINEAR_MIPMAP_LINEAR: Sample from mipmaps instead.

Before discussing mipmaps, let's first see the difference between nearest and linear interpolation. The original image is 16 times smaller than the rectangle it was rasterized on.

While linear interpolation gives a smoother result, it isn't always the most ideal option. Nearest neighbour interpolation is more suited in games that want to mimic 8 bit graphics, because of the pixelated look.

You can specify which kind of interpolation should be used for two separate cases: scaling the image down and scaling the image up. These two cases are identified by the keywords GL_TEXTURE_MIN_FILTER and GL_TEXTURE_MAG_FILTER.

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

As you've seen, there is another way to filter textures: mipmaps. Mipmaps are smaller copies of your texture that have been sized down and filtered in advance. It is recommended that you use them because they result in both a higher quality and higher performance.

glGenerateMipmap(GL_TEXTURE_2D);

Generating them is as simple as calling the function above, so there's no excuse for not using them! Note that you do have to load the texture image itself before mipmaps can be generated from it.

To use mipmaps, select one of the four mipmap filtering methods.

• GL_NEAREST_MIPMAP_NEAREST: Uses the mipmap that most closely matches the size of the pixel being textured and samples with nearest neighbour interpolation.
• GL_LINEAR_MIPMAP_NEAREST: Samples the closest mipmap with linear interpolation.
• GL_NEAREST_MIPMAP_LINEAR: Uses the two mipmaps that most closely match the size of the pixel being textured and samples with nearest neighbour interpolation.
• GL_LINEAR_MIPMAP_LINEAR: Samples closest two mipmaps with linear interpolation.

There are some other texture parameters available, but they're suited for specialized operations. You can read about them in the specification.

Loading texture images

Now that the texture object has been configured it's time to load the texture image. This is done by simply loading an array of pixels into it:

// Black/white checkerboard
float pixels[] = {
    0.0f, 0.0f, 0.0f,	1.0f, 1.0f, 1.0f,
    1.0f, 1.0f, 1.0f,	0.0f, 0.0f, 0.0f
};
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, 2, 2, 0, GL_RGB, GL_FLOAT, pixels);

The first parameter after the texture target is the level-of-detail, where 0 is the base image. This parameter can be used to load your own mipmap images. The second parameter specifies the internal pixel format, the format in which pixels should be stored on the graphics card. Many different formats are available, including compressed formats, so it's certainly worth taking a look at all of the options. The third and fourth parameters specify the width and height of the image. The fifth parameter should always have a value of 0 per the specification. The next two parameter describe the format of the pixels in the array that will be loaded and the final parameter specifies the array itself. The function begins loading the image at coordinate (0,0), so pay attention to this.

But how is the pixel array itself established? Textures in graphics applications will usually be a lot more sophisticated than simple patterns and will be loaded from files. Best practice is to have your files in a format that is natively supported by the hardware, but it may sometimes be more convenient to load textures from common image formats like JPG and PNG. Unfortunately OpenGL doesn't offer any helper functions to load pixels from these image files, but that's where third-party libraries come in handy again! The SOIL library will be discussed here along with some of the alternatives.

SOIL

SOIL (Simple OpenGL Image Library) is a small and easy-to-use library that loads image files directly into texture objects or creates them for you. You can start using it in your project by linking with SOIL and adding the src directory to your include path. It includes Visual Studio project files to compile it yourself.

Although SOIL includes functions to automatically create a texture from an image, it uses features that aren't available in modern OpenGL. Because of this we'll simply use SOIL as image loader and create the texture ourselves.

int width, height;
unsigned char* image =
    SOIL_load_image("img.png", &width, &height, 0, SOIL_LOAD_RGB);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB,
	  GL_UNSIGNED_BYTE, image);

You can start configuring the texture parameters and generating mipmaps after this.

SOIL_free_image_data(image);

You can clean up the image data right after you've loaded it into the texture.

As mentioned before, OpenGL expects the first pixel to be located in the bottom-left corner, which means that textures will be flipped when loaded with SOIL directly. To counteract that, the code in the tutorial will use flipped Y coordinates for texture coordinates from now on. That means that 0, 0 will be assumed to be the top-left corner instead of the bottom-left. This practice might make texture coordinates more intuitive as a side-effect.

Alternative options

Other libraries that support a wide range of file types like SOIL are DevIL and FreeImage. If you're just interested in one file type, it's also possible to use libraries like libpng and libjpeg directly. If you're looking for more of an adventure, have a look at the specification of the BMP and TGA file formats, it's not that hard to implement a loader for them yourself.

Using a texture

As you've seen, textures are sampled using texture coordinates and you'll have to add these as attributes to your vertices. Let's modify the last sample from the previous chapter to include these texture coordinates. The new vertex array will now include the s and t coordinates for each vertex:

float vertices[] = {
//  Position	  Color             Texcoords
    -0.5f,  0.5f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, // Top-left
     0.5f,  0.5f, 0.0f, 1.0f, 0.0f, 1.0f, 0.0f, // Top-right
     0.5f, -0.5f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f, // Bottom-right
    -0.5f, -0.5f, 1.0f, 1.0f, 1.0f, 0.0f, 1.0f  // Bottom-left
};

The vertex shader needs to be modified so that the texture coordinates are interpolated over the fragments:

...

in vec2 texcoord;

out vec3 Color;
out vec2 Texcoord;

...

void main()
{
    Texcoord = texcoord;

Just like when the color attribute was added, the attribute pointers need to be adapted to the new format:

glVertexAttribPointer(posAttrib, 2, GL_FLOAT, GL_FALSE,
				   7*sizeof(float), 0);
glVertexAttribPointer(colAttrib, 3, GL_FLOAT, GL_FALSE,
				   7*sizeof(float), (void*)(2*sizeof(float)));

GLint texAttrib = glGetAttribLocation(shaderProgram, "texcoord");
glEnableVertexAttribArray(texAttrib);
glVertexAttribPointer(texAttrib, 2, GL_FLOAT, GL_FALSE,
				   7*sizeof(float), (void*)(5*sizeof(float)));

As two floats were added for the coordinates, one vertex is now 7 floats in size and the texture coordinate attribute consists of 2 of those floats.

Now just one thing remains: providing access to the texture in the fragment shader to sample pixels from it. This is done by adding a uniform of type sampler2D, which will have a default value of 0. This only needs to be changed when access has to be provided to multiple textures, which will be considered in the next section.

For this sample, the image of the kitten used above will be loaded using the SOIL library. Make sure that it is located in the working directory of the application.

int width, height;
unsigned char* image =
    SOIL_load_image("sample.png", &width, &height, 0, SOIL_LOAD_RGB);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB,
  		  GL_UNSIGNED_BYTE, image);
SOIL_free_image_data(image);

To sample a pixel from a 2D texture using the sampler, the function texture can be called with the relevant sampler and texture coordinate as parameters. We'll also multiply the sampled color with the color attribute to get an interesting effect. Your fragment shader will now look like this:

#version 150 core

in vec3 Color;
in vec2 Texcoord;

out vec4 outColor;

uniform sampler2D tex;

void main()
{
    outColor = texture(tex, Texcoord) * vec4(Color, 1.0);
}

When running this application, you should get the following result:

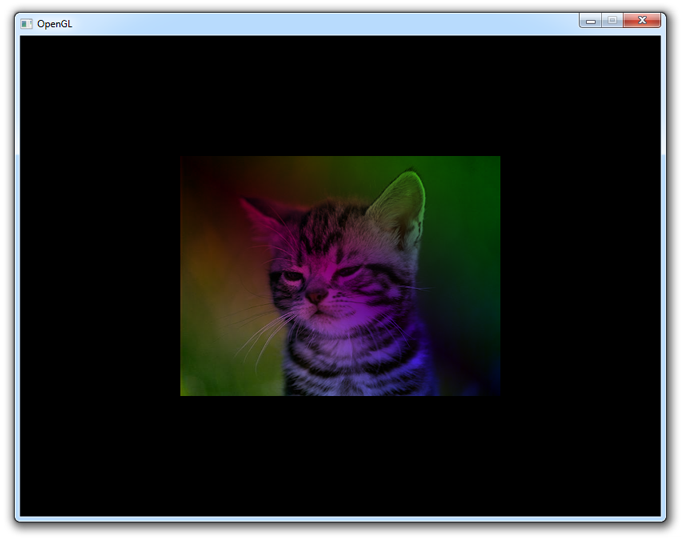
If you get a black screen, make sure that your shaders compiled successfully and that the image is correctly loaded. If you can't find the problem, try comparing your code to the sample code.

Texture units

The sampler in your fragment shader is bound to texture unit 0. Texture units are references to texture objects that can be sampled in a shader. Textures are bound to texture units using the glBindTexture function you've used before. Because you didn't explicitly specify which texture unit to use, the texture was bound to GL_TEXTURE0. That's why the default value of 0 for the sampler in your shader worked fine.

The function glActiveTexture specifies which texture unit a texture object is bound to when glBindTexture is called.

glActiveTexture(GL_TEXTURE0);

The amount of texture units supported differs per graphics card, but it will be at least 48. It is safe to say that you will never hit this limit in even the most extreme graphics applications.

To practice with sampling from multiple textures, let's try blending the images of the kitten and one of a puppy to get the best of both worlds! Let's first modify the fragment shader to sample from two textures and blend the pixels:

...

uniform sampler2D texKitten;
uniform sampler2D texPuppy;

void main()
{
    vec4 colKitten = texture(texKitten, Texcoord);
    vec4 colPuppy = texture(texPuppy, Texcoord);
    outColor = mix(colKitten, colPuppy, 0.5);
}

The mix function here is a special GLSL function that linearly interpolates between two variables based on the third parameter. A value of 0.0 will result in the first value, a value of 1.0 will result in the second value and a value in between will result in a mixture of both values. You'll have the chance to experiment with this in the exercises.

Now that the two samplers are ready, you'll have to assign the first two texture units to them and bind the two textures to those units. This is done by adding the proper glActiveTexture calls to the texture loading code.

GLuint textures[2];
glGenTextures(2, textures);

int width, height;
unsigned char* image;

glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, textures[0]);
image = SOIL_load_image("sample.png", &width, &height, 0, SOIL_LOAD_RGB);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB,
		  GL_UNSIGNED_BYTE, image);
SOIL_free_image_data(image);
glUniform1i(glGetUniformLocation(shaderProgram, "texKitten"), 0);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, textures[1]);
image = SOIL_load_image("sample2.png", &width, &height, 0, SOIL_LOAD_RGB);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB,
		  GL_UNSIGNED_BYTE, image);
SOIL_free_image_data(image);
glUniform1i(glGetUniformLocation(shaderProgram, "texPuppy"), 1);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

The texture units of the samplers are set using the glUniform function you've seen in the previous chapter. It simply accepts an integer specifying the texture unit. Make sure that at least the wrap texture parameters are set for both textures. This code should result in the following image.

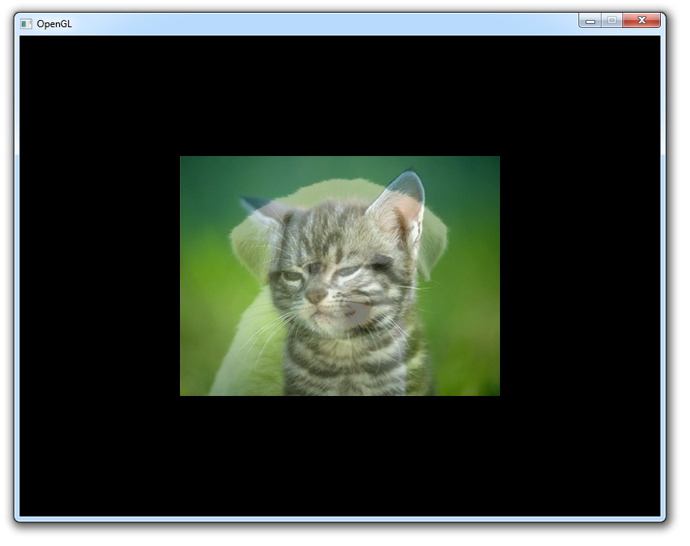
As always, have a look at the sample source code if you have trouble getting the program to work.

Now that texture sampling has been covered in this chapter, you're finally ready to dive into transformations and ultimately 3D. The knowledge you have at this point should be sufficient for producing most types of 2D games, except for transformations like rotation and scaling which will be covered in the next chapter.

Exercises

• Animate the blending between the textures by adding a time uniform. (Solution)
• Draw a reflection of the kitten in the lower half of the rectangle. (Solution)
• Now try adding distortion with sin and the time variable to simulate water. (Expected result, Solution)

Matrices

Since this is a guide on graphics programming, this chapter will not cover a lot of the extensive theory behind matrices. Only the theory that applies to their use in computer graphics will be considered here and they will be explained from a programmer's perspective. If you want to learn more about the topic, these Khan Academy videos are a really good general introduction to the subject.

A matrix is a rectangular array of mathematical expressions, much like a two-dimensional array. Below is an example of a matrix displayed in the common square brackets form.

$$a = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}$$

Matrices values are indexed by (i,j) where i is the row and j is the column. That is why the matrix displayed above is called a 3-by-2 matrix. To refer to a specific value in the matrix, for example 5, the (a_{31}) notation is used.

Basic operations

To get a bit more familiar with the concept of an array of numbers, let's first look at a few basic operations.

Addition and subtraction

Just like regular numbers, the addition and subtraction operators are also defined for matrices. The only requirement is that the two operands have exactly the same row and column dimensions.

$$ \begin{bmatrix} 3 & 2 \\ 0 & 4 \end{bmatrix} + \begin{bmatrix} 4 & 2 \\ 2 & 2 \end{bmatrix} = \begin{bmatrix} 3 + 4 & 2 + 2 \\ 0 + 2 & 4 + 2 \end{bmatrix} = \begin{bmatrix} 7 & 4 \\ 2 & 6 \end{bmatrix} $$ $$ \begin{bmatrix} 4 & 2 \\ 2 & 7 \end{bmatrix} \begin{bmatrix} 3 & 2 \\ 0 & 4 \end{bmatrix} = \begin{bmatrix} 4 - 3 & 2 - 2 \\ 2 - 0 & 7 - 4 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 2 & 3 \end{bmatrix} $$

The values in the matrices are individually added or subtracted from each other.

Scalar product

The product of a scalar and a matrix is as straightforward as addition and subtraction.

$$ 2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix} $$

The values in the matrices are each multiplied by the scalar.

Matrix-Vector product

The product of a matrix with another matrix is quite a bit more involved and is often misunderstood, so for simplicity's sake I will only mention the specific cases that apply to graphics programming. To see how matrices are actually used to transform vectors, we'll first dive into the product of a matrix and a vector.

$$ \begin{bmatrix} \color{red}a & \color{red}b & \color{red}c & \color{red}d \\ \color{blue}e & \color{blue}f & \color{blue}g & \color{blue}h \\ \color{green}i & \color{green}j & \color{green}k & \color{green}l \\ \color{magenta}m & \color{magenta}n & \color{magenta}o & \color{magenta}p \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}a\cdot x + \color{red}b\cdot y + \color{red}c\cdot z + \color{red}d\cdot 1 \\ \color{blue}e\cdot x + \color{blue}f\cdot y + \color{blue}g\cdot z + \color{blue}h\cdot 1 \\ \color{green}i\cdot x + \color{green}j\cdot y + \color{green}k\cdot z + \color{green}l\cdot 1 \\ \color{magenta}m\cdot x + \color{magenta}n\cdot y + \color{magenta}o\cdot z + \color{magenta}p\cdot 1 \end{pmatrix} $$

To calculate the product of a matrix and a vector, the vector is written as a 4-by-1 matrix. The expressions to the right of the equals sign show how the new x, y and z values are calculated after the vector has been transformed. For those among you who aren't very math savvy, the dot is a multiplication sign.

I will mention each of the common vector transformations in this section and how a matrix can be formed that performs them. For completeness, let's first consider a transformation that does absolutely nothing.

$$ \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 & \color{blue}0 \\ \color{green}0 & \color{green}0 & \color{green}1 & \color{green}0 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}1\cdot x + \color{red}0\cdot y + \color{red}0\cdot z + \color{red}0\cdot 1 \\ \color{blue}0\cdot x + \color{blue}1\cdot y + \color{blue}0\cdot z + \color{blue}0\cdot 1 \\ \color{green}0\cdot x + \color{green}0\cdot y + \color{green}1\cdot z + \color{green}0\cdot 1 \\ \color{magenta}0\cdot x + \color{magenta}0\cdot y + \color{magenta}0\cdot z + \color{magenta}1\cdot 1 \end{pmatrix} = \begin{pmatrix} \color{red}1\cdot x \\ \color{blue}1\cdot y \\ \color{green}1\cdot z \\ \color{magenta}1\cdot 1 \end{pmatrix} $$

This matrix is called the identity matrix, because just like the number 1, it will always return the value it was originally multiplied by. Let's look at the most common vector transformations now and deduce how a matrix can be formed from them. ### Translation To see why we're working with 4-by-1 vectors and subsequently 4-by-4 transformation matrices, let's see how a translation matrix is formed. A translation moves a vector a certain distance in a certain direction.

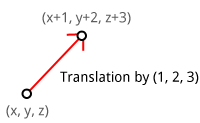
Can you guess from the multiplication overview what the matrix should look like to translate a vector by (X,Y,Z)?

$$ \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}X \\ \color{blue}0 & \color{blue}1 & \color{blue}0 & \color{blue}Y \\ \color{green}0 & \color{green}0 & \color{green}1 & \color{green}Z \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x+\color{red}X\cdot 1 \\ y+\color{blue}Y\cdot 1 \\ z+\color{green}Z\cdot 1 \\ 1 \end{pmatrix} $$

Without the fourth column and the bottom 1 value a translation wouldn't have been possible. ### Scaling A scale transformation scales each of a vector's components by a (different) scalar. It is commonly used to shrink or stretch a vector as demonstrated below.

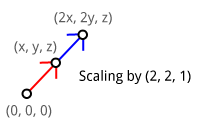
If you understand how the previous matrix was formed, it should not be difficult to come up with a matrix that scales a given vector by (SX,SY,SZ).

$$ \begin{bmatrix} \color{red}{SX} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{blue}0 & \color{blue}{SY} & \color{blue}0 & \color{blue}0 \\ \color{green}0 & \color{green}0 & \color{green}{SZ} & \color{green}0 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{SX}\cdot x \\ \color{green}{SY}\cdot y \\ \color{blue}{SZ}\cdot z \\ 1 \end{pmatrix} $$

If you think about it for a moment, you can see that scaling would also be possible with a mere 3-by-3 matrix. ### Rotation A rotation transformation rotates a vector around the origin (0,0,0) using a given axis and angle. To understand how the axis and the angle control a rotation, let's do a small experiment.

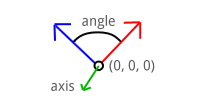
Put your thumb up against your monitor and try rotating your hand around it. The object, your hand, is rotating around your thumb: the rotation axis. The further you rotate your hand away from its initial position, the higher the rotation angle. In this way the rotation axis can be imagined as an arrow an object is rotating around. If you imagine your monitor to be a 2-dimensional XY surface, the rotation axis (your thumb) is pointing in the Z direction. Objects can be rotated around any given axis, but for now only the X, Y and Z axis are important. You'll see later in this chapter that any rotation axis can be established by rotating around the X, Y and Z axis simultaneously.

The matrices for rotating around the three axes are specified here. The rotation angle is indicated by the theta (θ).

Rotation around X-axis:

$$ \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{blue}0 & \color{blue}{\cos\theta} & \color{blue}{-\sin\theta} & \color{blue}0 \\ \color{green}0 & \color{green}{\sin\theta} & \color{green}{\cos\theta} & \color{green}0 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \color{blue}{\cos\theta}\cdot y \color{blue}{-\sin\theta}\cdot z \\ \color{green}{\sin\theta}\cdot y + \color{green}{\cos\theta}\cdot z \\ 1 \end{pmatrix} $$

Rotation around Y-axis:

$$ \begin{bmatrix} \color{red}{\cos\theta} & \color{red}0 & \color{red}{\sin\theta} & \color{red}0 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 & \color{blue}0 \\ \color{green}{-\sin\theta} & \color{green}0 & \color{green}{\cos\theta} & \color{green}0 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos\theta}\cdot x + \color{red}{\sin\theta}\cdot z \\ y \\ \color{green}{-\sin\theta}\cdot x + \color{green}{\cos\theta}\cdot z \\ 1 \end{pmatrix} $$

Rotation around Z-axis:

$$ \begin{bmatrix} \color{red}{\cos\theta} & \color{red}{-\sin\theta} & \color{red}0 & \color{red}0 \\ \color{blue}{\sin\theta} & \color{blue}{\cos\theta} & \color{blue}0 & \color{blue}0 \\ \color{green}0 & \color{green}0 & \color{green}1 & \color{green}0 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos\theta}\cdot x \color{red}{-\sin\theta}\cdot y \\ \color{blue}{\sin\theta}\cdot x + \color{blue}{\cos\theta}\cdot y \\ z \\ 1 \end{pmatrix} $$

Don't worry about understanding the actual geometry behind this, explaining that is beyond the scope of this guide. What matters is that you have a solid idea of how a rotation is described by a rotation axis and an angle and that you've at least seen what a rotation matrix looks like.

Matrix-Matrix product

In the previous section you've seen how transformation matrices can be used to apply transformations to vectors, but this by itself is not very useful. It clearly takes far less effort to do a translation and scaling by hand without all those pesky matrices!

Now, what if I told you that it is possible to combine as many transformations as you want into a single matrix by simply multiplying them? You would be able to apply even the most complex transformations to any vertex with a simple multiplication.

In the same style as the previous section, this is how the product of two 4-by-4 matrices is determined:

$$ \begin{bmatrix} \color{red}a & \color{red}b & \color{red}c & \color{red}d \\ \color{blue}e & \color{blue}f & \color{blue}g & \color{blue}h \\ \color{green}i & \color{green}j & \color{green}k & \color{green}l \\ \color{magenta}m & \color{magenta}n & \color{magenta}o & \color{magenta}p \end{bmatrix} \cdot \begin{bmatrix} \color{red}A & \color{blue}B & \color{green}C & \color{magenta}D \\ \color{red}E & \color{blue}F & \color{green}G & \color{magenta}H \\ \color{red}I & \color{blue}J & \color{green}K & \color{magenta}L \\ \color{red}M & \color{blue}N & \color{green}O & \color{magenta}P \end{bmatrix} = \\ \begin{bmatrix} \color{red}{aA} + \color{red}{bE} + \color{red}{cI} + \color{red}{dM} & \color{red}a\color{blue}B + \color{red}b\color{blue}F + \color{red}c\color{blue}J + \color{red}d\color{blue}N & \color{red}a\color{green}C + \color{red}b\color{green}G + \color{red}c\color{green}K + \color{red}d\color{green}O & \color{red}a\color{magenta}D + \color{red}b\color{magenta}H + \color{red}c\color{magenta}L + \color{red}d\color{magenta}P \\ \color{blue}e\color{red}A + \color{blue}f\color{red}E + \color{blue}g\color{red}I + \color{blue}h\color{red}M & \color{blue}{eB} + \color{blue}{fF} + \color{blue}{gJ} + \color{blue}{hN} & \color{blue}e\color{green}C + \color{blue}f\color{green}G + \color{blue}g\color{green}K + \color{blue}h\color{green}O & \color{blue}e\color{magenta}D + \color{blue}f\color{magenta}H + \color{blue}g\color{magenta}L + \color{blue}h\color{magenta}P \\ \color{green}i\color{red}A + \color{green}j\color{red}E + \color{green}k\color{red}I + \color{green}l\color{red}M & \color{green}i\color{blue}B + \color{green}j\color{blue}F + \color{green}k\color{blue}J + \color{green}l\color{blue}N & \color{green}{iC} + \color{green}{jG} + \color{green}{kK} + \color{green}{lO} & \color{green}i\color{magenta}D + \color{green}j\color{magenta}H + \color{green}k\color{magenta}L + \color{green}l\color{magenta}P \\ \color{magenta}m\color{red}A + \color{magenta}n\color{red}E + \color{magenta}o\color{red}I + \color{magenta}p\color{red}M & \color{magenta}m\color{blue}B + \color{magenta}n\color{blue}F + \color{magenta}o\color{blue}J + \color{magenta}p\color{blue}N & \color{magenta}m\color{green}C + \color{magenta}n\color{green}G + \color{magenta}o\color{green}K + \color{magenta}p\color{green}O & \color{magenta}{mD} + \color{magenta}{nH} + \color{magenta}{oL} + \color{magenta}{pP} \end{bmatrix} $$

The above is commonly recognized among mathematicians as an indecipherable mess. To get a better idea of what's going on, let's consider two 2-by-2 matrices instead.

$$ \begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{blue}3 & \color{blue}4 \end{bmatrix} \cdot \begin{bmatrix} \color{green}a & \color{magenta}b \\ \color{green}c & \color{magenta}d \end{bmatrix} = \begin{bmatrix} \color{red}1\cdot \color{green}a + \color{red}2 \cdot \color{green}c & \color{red}1 \cdot \color{magenta}b + \color{red}2 \cdot \color{magenta}d \\ \color{blue}3\cdot \color{green}a + \color{blue}4 \cdot \color{green}c & \color{blue}3 \cdot \color{magenta}b + \color{blue}4 \cdot \color{magenta}d \end{bmatrix} $$

Try to see the pattern here with help of the colors. The factors on the left side (1,2 and 3,4) of the multiplication dot are the values in the row of the first matrix. The factors on the right side are the values in the rows of the second matrix repeatedly. It is not necessary to remember how exactly this works, but it's good to have seen how it's done at least once.

Combining transformations

To demonstrate the multiplication of two matrices, let's try scaling a given vector by (2,2,2) and translating it by (1,2,3). Given the translation and scaling matrices above, the following product is calculated:

$$ M*\text{translate}\cdot M*\text{scale} = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 & \color{blue}2 \\ \color{green}0 & \color{green}0 & \color{green}1 & \color{green}3 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{bmatrix} \color{red}{2} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{blue}0 & \color{blue}{2} & \color{blue}0 & \color{blue}0 \\ \color{green}0 & \color{green}0 & \color{green}{2} & \color{green}0 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} = \begin{bmatrix} \color{red}{2} & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{blue}0 & \color{blue}{2} & \color{blue}0 & \color{blue}2 \\ \color{green}0 & \color{green}0 & \color{green}{2} & \color{green}3 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} $$

Notice how we want to scale the vector first, but the scale transformation comes last in the multiplication. Pay attention to this when combining transformations or you'll get the opposite of what you've asked for.

Now, let's try to transform a vector and see if it worked:

$$ \begin{bmatrix} \color{red}{2} & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{blue}0 & \color{blue}{2} & \color{blue}0 & \color{blue}2 \\ \color{green}0 & \color{green}0 & \color{green}{2} & \color{green}3 \\ \color{magenta}0 & \color{magenta}0 & \color{magenta}0 & \color{magenta}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}2 x + \color{red}1 \\ \color{blue}2y + \color{blue}2 \\ \color{green}2z + \color{green}3 \\ 1 \end{pmatrix} $$

Perfect! The vector is first scaled by two and then shifted in position by (1,2,3).

Transformations in OpenGL

You've seen in the previous sections how basic transformations can be applied to vectors to move them around in the world. The job of transforming 3D points into 2D coordinates on your screen is also accomplished through matrix transformations. Just like the graphics pipeline, transforming a vector is done step-by-step. Although OpenGL allows you to decide on these steps yourself, all 3D graphics applications use a variation of the process described here.

Each transformation transforms a vector into a new coordinate system, thus moving to the next step. These transformations and coordinate systems will be discussed below in more detail.

Model matrix

The model matrix transforms a position in a model to the position in the world. This position is affected by the position, scale and rotation of the model that is being drawn. It is generally a combination of the simple transformations you've seen before. If you are already specifying your vertices in world coordinates (common when drawing a simple test scene), then this matrix can simply be set to the identity matrix.

View matrix

In real life you're used to moving the camera to alter the view of a certain scene, in OpenGL it's the other way around. The camera in OpenGL cannot move and is defined to be located at (0,0,0) facing the negative Z direction. That means that instead of moving and rotating the camera, the world is moved and rotated around the camera to construct the appropriate view.

Older versions of OpenGL forced you to use ModelView and Projection transformations. The ModelView matrix combined the model and view transformations into one. I personally find it is easier to separate the two, so the view transformation can be modified independently of the model matrix.

That means that to simulate a camera transformation, you actually have to transform the world with the inverse of that transformation. Example: if you want to move the camera up, you have to move the world down instead.

Projection matrix

After the world has been aligned with your camera using the view transformation, the projection transformation can be applied, resulting in the clip coordinates. If you're doing a perspective transformation, these clip coordinates are not ready to be used as normalized device coordinates just yet.

To transform the clipping coordinate into a normalized device coordinate, perspective division has to be performed. A clipping coordinate resulting from a perspective projection has a number different than 1 in the fourth row, also known as w. This number directly reflects the effect of objects further away being smaller than those up front.

$$ v_\text{normalized} = \begin{pmatrix} x_\text{clip} / w_\text{clip} \ y_\text{clip} / w_\text{clip} \ z_\text{clip} / w_\text{clip} \end{pmatrix} $$

The x and y coordinates will be in the familiar -1 and 1 range now, which OpenGL can transform into window coordinates. The z is known as the depth and will play an important role in the next chapter.

The coordinates resulting from the projection transformation are called clipping coordinates because the value of w is used to determine whether an object is too close or behind the camera or too far away to be drawn. The projection matrix is created with those limits, so you'll be able to specify these yourself.

Putting it all together

To sum it all up, the final transformation of a vertex is the product of the model, view and projection matrices.

$$ v' = M_\text{proj} \cdot M_\text{view} \cdot M_\text{model} \cdot v $$

This operation is typically performed in the vertex shader and assigned to the gl_Position return value in clipping coordinates. OpenGL will perform the perspective division and transformation into window coordinates. It is important to be aware of these steps, because you'll have to do them yourself when working with techniques like shadow mapping.

Using transformations for 3D

Now that you know three important transformations, it is time to implement these in code to create an actual 3D scene. You can use any of the programs developed in the last two chapters as a base, but I'll use the texture blending sample from the end of the last chapter here.

To introduce matrices in the code, we can make use of the GLM (OpenGL Math) library. This library comes with vector and matrix classes and will handle all the math efficiently without ever having to worry about it. It is a header-only library, which means you don't have to link with anything.

To use it, add the GLM root directory to your include path and include these three headers:

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

The second header includes functions to ease the calculation of the view and projection matrices. The third header adds functionality for converting a matrix object into a float array for usage in OpenGL.

A simple transformation

Before diving straight into 3D, let's first try a simple 2D rotation.

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(180.0f), glm::vec3(0.0f, 0.0f, 1.0f));

The first line creates a new 4-by-4 matrix and initializes it to the identity matrix. The glm::rotate function multiplies this matrix by a rotation transformation of 180 degrees around the Z axis. Remember that since the screen lies in the XY plane, the Z axis is the axis you want to rotate points around.

To see if it works, let's try to rotate a vector with this transformation:

glm::vec4 result = trans * glm::vec4(1.0f, 0.0f, 0.0f, 1.0f);
printf("%f, %f, %f\n", result.x, result.y, result.z);

As expected, the output is (-1,0,0). A counter-clockwise rotation of 180 degrees of a vector pointing to the right results in a vector pointing to the left. Note that the rotation would be clockwise if an axis (0,0,-1) was used.

The next step is to perform this transformation in the vertex shader to rotate every drawn vertex. GLSL has a special mat4 type to hold matrices and we can use that to upload the transformation to the GPU as uniform.

GLint uniTrans = glGetUniformLocation(shaderProgram, "trans");
glUniformMatrix4fv(uniTrans, 1, GL_FALSE, glm::value_ptr(trans));

The second parameter of the glUniformMatrix4fv function specifies how many matrices are to be uploaded, because you can have arrays of matrices in GLSL. The third parameter specifies whether the specified matrix should be transposed before usage. This is related to the way matrices are stored as float arrays in memory; you don't have to worry about it. The last parameter specifies the matrix to upload, where the glm::value_ptr function converts the matrix class into an array of 16 (4x4) floats.

All that remains is updating the vertex shader to include this uniform and use it to transform each vertex:

#version 150 core

in vec2 position;
in vec3 color;
in vec2 texcoord;

out vec3 Color;
out vec2 Texcoord;

uniform mat4 trans;

void main()
{
    Color = color;
    Texcoord = texcoord;
    gl_Position = trans * vec4(position, 0.0, 1.0);
}

The primitives in your scene will now be upside down.

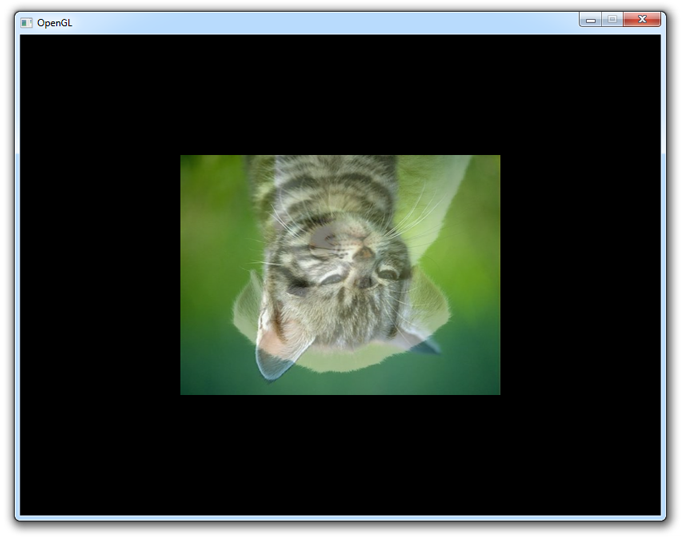
To spice things up a bit, you could change the rotation with time:

auto t_start = std::chrono::high_resolution_clock::now();

...

// Calculate transformation
auto t_now = std::chrono::high_resolution_clock::now();
float time = std::chrono::duration_cast<std::chrono::duration<float>>(t_now - t_start).count();

glm::mat4 trans;
trans = glm::rotate(
    trans,
    time * glm::radians(180.0f),
    glm::vec3(0.0f, 0.0f, 1.0f)
);
glUniformMatrix4fv(uniTrans, 1, GL_FALSE, glm::value_ptr(trans));

// Draw a rectangle from the 2 triangles using 6 indices
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);

...

This will result in something like this:

You can find the full code here if you have any issues.

Going 3D

The rotation above can be considered the model transformation, because it transforms the vertices in object space to world space using the rotation of the object.

glm::mat4 view = glm::lookAt(
    glm::vec3(1.2f, 1.2f, 1.2f),
    glm::vec3(0.0f, 0.0f, 0.0f),
    glm::vec3(0.0f, 0.0f, 1.0f)
);
GLint uniView = glGetUniformLocation(shaderProgram, "view");
glUniformMatrix4fv(uniView, 1, GL_FALSE, glm::value_ptr(view));

To create the view transformation, GLM offers the useful glm::lookAt function that simulates a moving camera. The first parameter specifies the position of the camera, the second the point to be centered on-screen and the third the up axis. Here up is defined as the Z axis, which implies that the XY plane is the "ground".

glm::mat4 proj = glm::perspective(glm::radians(45.0f), 800.0f / 600.0f, 1.0f, 10.0f);
GLint uniProj = glGetUniformLocation(shaderProgram, "proj");
glUniformMatrix4fv(uniProj, 1, GL_FALSE, glm::value_ptr(proj));

Similarly, GLM comes with the glm::perspective function to create a perspective projection matrix. The first parameter is the vertical field-of-view, the second parameter the aspect ratio of the screen and the last two parameters are the near and far planes.

Field-of-view

The field-of-view defines the angle between the top and bottom of the 2D surface on which the world will be projected. Zooming in games is often accomplished by decreasing this angle as opposed to moving the camera closer, because it more closely resembles real life.

By decreasing the angle, you can imagine that the "rays" from the camera spread out less and thus cover a smaller area of the scene.

The near and far planes are known as the clipping planes. Any vertex closer to the camera than the near clipping plane and any vertex farther away than the far clipping plane is clipped as these influence the w value.

Now piecing it all together, the vertex shader looks something like this:

#version 150 core

in vec2 position;
in vec3 color;
in vec2 texcoord;

out vec3 Color;
out vec2 Texcoord;

uniform mat4 model;
uniform mat4 view;
uniform mat4 proj;

void main()
{
    Color = color;
    Texcoord = texcoord;
    gl_Position = proj * view * model * vec4(position, 0.0, 1.0);
}

Notice that I've renamed the matrix previously known as trans to model and it is still updated every frame.

Success! You can find the full code here if you get stuck.

Exercises

• Make the rectangle with the blended image grow bigger and smaller with sin. (Solution)
• Make the rectangle flip around the X axis after pressing the space bar and slowly stop again. (Solution)

Extra buffers

Up until now there is only one type of output buffer you've made use of, the color buffer. This chapter will discuss two additional types, the depth buffer and the stencil buffer. For each of these a problem will be presented and subsequently solved with that specific buffer.

Preparations

To best demonstrate the use of these buffers, let's draw a cube instead of a flat shape. The vertex shader needs to be modified to accept a third coordinate:

in vec3 position;
...
gl_Position = proj * view * model * vec4(position, 1.0);

We're also going to need to alter the color again later in this chapter, so make sure the fragment shader multiplies the texture color by the color attribute:

vec4 texColor = mix(texture(texKitten, Texcoord),
					 texture(texPuppy, Texcoord), 0.5);
outColor = vec4(Color, 1.0) * texColor;

Vertices are now 8 floats in size, so you'll have to update the vertex attribute offsets and strides as well. Finally, add the extra coordinate to the vertex array:

float vertices[] = {
  // X      Y     Z     R     G     B     U     V
	-0.5f,  0.5f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f,
	 0.5f,  0.5f, 0.0f, 0.0f, 1.0f, 0.0f, 1.0f, 0.0f,
	 0.5f, -0.5f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f, 1.0f,
	-0.5f, -0.5f, 0.0f, 1.0f, 1.0f, 1.0f, 0.0f, 1.0f
};

Confirm that you've made all the required changes by running your program and checking if it still draws a flat spinning image of a kitten blended with a puppy. A single cube consists of 36 vertices (6 sides _ 2 triangles _ 3 vertices), so I will ease your life by providing the array here.

glDrawArrays(GL_TRIANGLES, 0, 36);

We will not make use of element buffers for drawing this cube, so you can use glDrawArrays to draw it. If you were confused by this explanation, you can compare your program to this reference code.

It immediately becomes clear that the cube is not rendered as expected when seeing the output. The sides of the cube are being drawn, but they overlap each other in strange ways! The problem here is that when OpenGL draws your cube triangle-by-triangle, it will simply write over pixels even though something else may have been drawn there before. In this case OpenGL will happily draw triangles in the back over triangles at the front.

Luckily OpenGL offers ways of telling it when to draw over a pixel and when not to. I'll go over the two most important ways of doing that, depth testing and stencilling, in this chapter.

Depth buffer

Z-buffering is a way of keeping track of the depth of every pixel on the screen. The depth is an increasing function of the distance between the screen plane and a fragment that has been drawn. That means that the fragments on the sides of the cube further away from the viewer have a higher depth value, whereas fragments closer have a lower depth value.

If this depth is stored along with the color when a fragment is written, fragments drawn later can compare their depth to the existing depth to determine if the new fragment is closer to the viewer than the old fragment. If that is the case, it should be drawn over and otherwise it can simply be discarded. This is known as depth testing.

OpenGL offers a way to store these depth values in an extra buffer, called the depth buffer, and perform the required check for fragments automatically. The fragment shader will not run for fragments that are invisible, which can have a significant impact on performance. This functionality can be enabled by calling glEnable.

glEnable(GL_DEPTH_TEST);

If you enable this functionality now and run your application, you'll notice that you get a black screen. That happens because the depth buffer is filled with 0 depth for each pixel by default. Since no fragments will ever be closer than that they are all discarded.

The depth buffer can be cleared along with the color buffer by extending the glClear call:

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

The default clear value for the depth is 1.0f, which is equal to the depth of your far clipping plane and thus the furthest depth that can be represented. All fragments will be closer than that, so they will no longer be discarded.

With the depth test capability enabled, the cube is now rendered correctly. Just like the color buffer, the depth buffer has a certain amount of bits of precision which can be specified by you. Less bits of precision reduce the extra memory use, but can introduce rendering errors in more complex scenes.

Stencil buffer

The stencil buffer is an optional extension of the depth buffer that gives you more control over the question of which fragments should be drawn and which shouldn't. Like the depth buffer, a value is stored for every pixel, but this time you get to control when and how this value changes and when a fragment should be drawn depending on this value. Note that if the depth test fails, the stencil test no longer determines whether a fragment is drawn or not, but these fragments can still affect values in the stencil buffer!

To get a bit more acquainted with the stencil buffer before using it, let's start by analyzing a simple example.

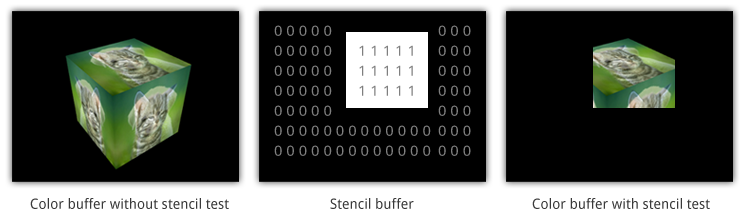
In this case the stencil buffer was first cleared with zeroes and then a rectangle of ones was drawn to it. The drawing operation of the cube uses the values from the stencil buffer to only draw fragments with a stencil value of 1.

Now that you have an understanding of what the stencil buffer does, we'll look at the relevant OpenGL calls.

glEnable(GL_STENCIL_TEST);

Stencil testing is enabled with a call to glEnable, just like depth testing. You don't have to add this call to your code just yet. I'll first go over the API details in the next two sections and then we'll make a cool demo.

Setting values

Regular drawing operations are used to determine which values in the stencil buffer are affected by any stencil operation. If you want to affect a rectangle of values like in the sample above, simply draw a 2D quad in that area. What happens to those values can be controlled by you using the glStencilFunc, glStencilOp and glStencilMask functions.

The glStencilFunc call is used to specify the conditions under which a fragment passes the stencil test. Its parameters are discussed below.

• func: The test function, can be GL_NEVER, GL_LESS, GL_LEQUAL, GL_GREATER, GL_GEQUAL, GL_EQUAL, GL_NOTEQUAL, and GL_ALWAYS.
• ref: A value to compare the stencil value to using the test function.
• mask: A bitwise AND operation is performed on the stencil value and reference value with this mask value before comparing them.

If you don't want stencils with a value lower than 2 to be affected, you would use:

glStencilFunc(GL_GEQUAL, 2, 0xFF);

The mask value is set to all ones (in case of an 8 bit stencil buffer), so it will not affect the test.

The glStencilOp call specifies what should happen to stencil values depending on the outcome of the stencil and depth tests. The parameters are:

• sfail: Action to take if the stencil test fails.
• dpfail: Action to take if the stencil test is successful, but the depth test failed.
• dppass: Action to take if both the stencil test and depth tests pass.

Stencil values can be modified in the following ways:

• GL_KEEP: The current value is kept.
• GL_ZERO: The stencil value is set to 0.
• GL_REPLACE: The stencil value is set to the reference value in the glStencilFunc call.
• GL_INCR: The stencil value is increased by 1 if it is lower than the maximum value.
• GL_INCR_WRAP: Same as GL_INCR, with the exception that the value is set to 0 if the maximum value is exceeded.
• GL_DECR: The stencil value is decreased by 1 if it is higher than 0.
• GL_DECR_WRAP: Same as GL_DECR, with the exception that the value is set to the maximum value if the current value is 0 (the stencil buffer stores unsigned integers).
• GL_INVERT: A bitwise invert is applied to the value.

Finally, glStencilMask can be used to control the bits that are written to the stencil buffer when an operation is run. The default value is all ones, which means that the outcome of any operation is unaffected.

If, like in the example, you want to set all stencil values in a rectangular area to 1, you would use the following calls:

glStencilFunc(GL_ALWAYS, 1, 0xFF);
glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);
glStencilMask(0xFF);

In this case the rectangle shouldn't actually be drawn to the color buffer, since it is only used to determine which stencil values should be affected.

glColorMask(GL_FALSE, GL_FALSE, GL_FALSE, GL_FALSE);
glDepthMask(GL_FALSE);

The glColorMask function allows you to specify which data is written to the color buffer during a drawing operation. In this case you would want to disable all color channels (red, green, blue, alpha). Writing to the depth buffer needs to be disabled separately as well with glDepthMask, so that cube drawing operation won't be affected by leftover depth values of the rectangle. This is cleaner than simply clearing the depth buffer again later.

Using values in drawing operations

With the knowledge about setting values, using them for testing fragments in drawing operations becomes very simple. All you need to do now is re-enable color and depth writing if you had disabled those earlier and setting the test function to determine which fragments are drawn based on the values in the stencil buffer.

glStencilFunc(GL_EQUAL, 1, 0xFF);

If you use this call to set the test function, the stencil test will only pass for pixels with a stencil value equal to 1. A fragment will only be drawn if it passes both the stencil and depth test, so setting the glStencilOp is not necessary. In the case of the example above only the stencil values in the rectangular area were set to 1, so only the cube fragments in that area will be drawn.

glStencilMask(0x00);

One small detail that is easy to overlook is that the cube draw call could still affect values in the stencil buffer. This problem can be solved by setting the stencil bit mask to all zeroes, which effectively disables stencil writing.

Planar reflections

Let's spice up the demo we have right now a bit by adding a floor with a reflection under the cube. I'll add the vertices for the floor to the same vertex buffer the cube is currently using to keep things simple:

float vertices[] = {
    ...

    -1.0f, -1.0f, -0.5f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f,
     1.0f, -1.0f, -0.5f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f,
     1.0f,  1.0f, -0.5f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f,
     1.0f,  1.0f, -0.5f, 0.0f, 0.0f, 0.0f, 1.0f, 1.0f,
    -1.0f,  1.0f, -0.5f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f,
    -1.0f, -1.0f, -0.5f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f
}

Now add the extra draw call to your main loop:

glDrawArrays(GL_TRIANGLES, 36, 6);

To create the reflection of the cube itself, it is sufficient to draw it again but inverted on the Z-axis:

model = glm::scale(
    glm::translate(model, glm::vec3(0, 0, -1)),
    glm::vec3(1, 1, -1)
);
glUniformMatrix4fv(uniModel, 1, GL_FALSE, glm::value_ptr(model));
glDrawArrays(GL_TRIANGLES, 0, 36);

I've set the color of the floor vertices to black so that the floor does not display the texture image, so you'll want to change the clear color to white to be able to see it. I've also changed the camera parameters a bit to get a good view of the scene.

Two issues are noticeable in the rendered image:

• The floor occludes the reflection because of depth testing.
• The reflection is visible outside of the floor.

The first problem is easy to solve by temporarily disabling writing to the depth buffer when drawing the floor:

glDepthMask(GL_FALSE);
glDrawArrays(GL_TRIANGLES, 36, 6);
glDepthMask(GL_TRUE);

To fix the second problem, it is necessary to discard fragments that fall outside of the floor. Sounds like it's time to see what stencil testing is really worth!

It can be greatly beneficial at times like these to make a little list of the rendering stages of the scene to get a proper idea of what is going on.

• Draw regular cube.
• Enable stencil testing and set test function and operations to write ones to all selected stencils.
• Draw floor.
• Set stencil function to pass if stencil value equals 1.
• Draw inverted cube.
• Disable stencil testing.

The new drawing code looks like this:

glEnable(GL_STENCIL_TEST);

    // Draw floor
    glStencilFunc(GL_ALWAYS, 1, 0xFF); // Set any stencil to 1
    glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);
    glStencilMask(0xFF); // Write to stencil buffer
    glDepthMask(GL_FALSE); // Don't write to depth buffer
    glClear(GL_STENCIL_BUFFER_BIT); // Clear stencil buffer (0 by default)

    glDrawArrays(GL_TRIANGLES, 36, 6);

    // Draw cube reflection
    glStencilFunc(GL_EQUAL, 1, 0xFF); // Pass test if stencil value is 1
    glStencilMask(0x00); // Don't write anything to stencil buffer
    glDepthMask(GL_TRUE); // Write to depth buffer

    model = glm::scale(
    	glm::translate(model, glm::vec3(0, 0, -1)),
    	glm::vec3(1, 1, -1)
    );
    glUniformMatrix4fv(uniModel, 1, GL_FALSE, glm::value_ptr(model));
    glDrawArrays(GL_TRIANGLES, 0, 36);

    glDisable(GL_STENCIL_TEST);

I've annotated the code above with comments, but the steps should be mostly clear from the stencil buffer section.

Now just one final touch is required, to darken the reflected cube a little to make the floor look a little less like a perfect mirror. I've chosen to create a uniform for this called overrideColor in the vertex shader:

uniform vec3 overrideColor;
...
Color = overrideColor * color;

And in the drawing code for the reflected cube

glUniform3f(uniColor, 0.3f, 0.3f, 0.3f);
    glDrawArrays(GL_TRIANGLES, 0, 36);
glUniform3f(uniColor, 1.0f, 1.0f, 1.0f);

where uniColor is the return value of a glGetUniformLocation call.

Awesome! I hope that, especially in chapters like these, you get the idea that working with an API as low-level as OpenGL can be a lot of fun and pose interesting challenges! As usual, the final code is available here.

Exercises

There are no real exercises for this chapter, but there are a lot more interesting effects you can create with the stencil buffer. I'll leave researching the implementation of other effects, such as stencil shadows and object outlining as an exercise to you.

Framebuffers

In the previous chapters we've looked at the different types of buffers OpenGL offers: the color, depth and stencil buffers. These buffers occupy video memory like any other OpenGL object, but so far we've had little control over them besides specifying the pixel formats when you created the OpenGL context. This combination of buffers is known as the default framebuffer and as you've seen, a framebuffer is an area in memory that can be rendered to. What if you want to take a rendered result and do some additional operations on it, such as post-processing as seen in many modern games?

In this chapter we'll look at framebuffer objects, which are a means of creating additional framebuffers to render to. The great thing about framebuffers is that they allow you to render a scene directly to a texture, which can then be used in other rendering operations. After discussing how framebuffer objects work, I'll show you how to use them to do post-processing on the scene from the previous chapter.

Creating a new framebuffer

The first thing you need is a framebuffer object to manage your new framebuffer.

GLuint frameBuffer;
glGenFramebuffers(1, &frameBuffer);

You can not use this framebuffer yet at this point, because it is not complete. A framebuffer is generally complete if:

• At least one buffer has been attached (e.g. color, depth, stencil)
• There must be at least one color attachment (OpenGL 4.1 and earlier)
• All attachments are complete (For example, a texture attachment needs to have memory reserved)
• All attachments must have the same number of multisamples

You can check if a framebuffer is complete at any time by calling glCheckFramebufferStatus and check if it returns GL_FRAMEBUFFER_COMPLETE. See the reference for other return values. You don't have to do this check, but it's usually a good thing to verify, just like checking if your shaders compiled successfully.

Now, let's bind the framebuffer to work with it.

glBindFramebuffer(GL_FRAMEBUFFER, frameBuffer);

The first parameter specifies the target the framebuffer should be attached to. OpenGL makes a distinction here between GL_DRAW_FRAMEBUFFER and GL_READ_FRAMEBUFFER. The framebuffer bound to read is used in calls to glReadPixels, but since this distinction in normal applications is fairly rare, you can have your actions apply to both by using GL_FRAMEBUFFER.

glDeleteFramebuffers(1, &frameBuffer);

Don't forget to clean up after you're done.

Attachments

Your framebuffer can only be used as a render target if memory has been allocated to store the results. This is done by attaching images for each buffer (color, depth, stencil or a combination of depth and stencil). There are two kinds of objects that can function as images: texture objects and renderbuffer objects. The advantage of the former is that they can be directly used in shaders as seen in the previous chapters, but renderbuffer objects may be more optimized specifically as render targets depending on your implementation.

Texture images

We'd like to be able to render a scene and then use the result in the color buffer in another rendering operation, so a texture is ideal in this case. Creating a texture for use as an image for the color buffer of the new framebuffer is as simple as creating any texture.

GLuint texColorBuffer;
glGenTextures(1, &texColorBuffer);
glBindTexture(GL_TEXTURE_2D, texColorBuffer);

glTexImage2D(
    GL_TEXTURE_2D, 0, GL_RGB, 800, 600, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL
);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

The difference between this texture and the textures you've seen before is the NULL value for the data parameter. That makes sense, because the data is going to be created dynamically this time with rendering operations. Since this is the image for the color buffer, the format and internalformat parameters are a bit more restricted. The format parameter will typically be limited to either GL_RGB or GL_RGBA and the internalformat to the color formats.

I've chosen the default RGB internal format here, but you can experiment with more exotic formats like GL_RGB10 if you want 10 bits of color precision. My application has a resolution of 800 by 600 pixels, so I've made this new color buffer match that. The resolution doesn't have to match the one of the default framebuffer, but don't forget a glViewport call if you do decide to vary.

The one thing that remains is attaching the image to the framebuffer.

glFramebufferTexture2D(
    GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_2D, texColorBuffer, 0
);

The second parameter implies that you can have multiple color attachments. A fragment shader can output different data to any of these by linking out variables to attachments with the glBindFragDataLocation function we used earlier. We'll stick to one output for now. The last parameter specifies the mipmap level the image should be attached to. Mipmapping is not of any use, since the color buffer image will be rendered at its original size when using it for post-processing.

Renderbuffer Object images

As we're using a depth and stencil buffer to render the spinning cube of cuteness, we'll have to create them as well. OpenGL allows you to combine those into one image, so we'll have to create just one more before we can use the framebuffer. Although we could do this by creating another texture, it is more efficient to store these buffers in a Renderbuffer Object, because we're only interested in reading the color buffer in a shader.

GLuint rboDepthStencil;
glGenRenderbuffers(1, &rboDepthStencil);
glBindRenderbuffer(GL_RENDERBUFFER, rboDepthStencil);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH24_STENCIL8, 800, 600);

Creating a renderbuffer object is very similar to creating a texture, the difference being is that this object is designed to be used as image instead of a general purpose data buffer like a texture. I've chosen the GL_DEPTH24_STENCIL8 internal format here, which is suited for holding both the depth and stencil buffer with 24 and 8 bits of precision respectively.

glFramebufferRenderbuffer(
    GL_FRAMEBUFFER, GL_DEPTH_STENCIL_ATTACHMENT, GL_RENDERBUFFER, rboDepthStencil
);

Attaching it is easy as well. You can delete this object like any other object at a later time with a call to glDeleteRenderbuffers.

Using a framebuffer

Selecting a framebuffer as render target is very easy, in fact it can be done with a single call.

glBindFramebuffer(GL_FRAMEBUFFER, frameBuffer);

After this call, all rendering operations will store their result in the attachments of the newly created framebuffer. To switch back to the default framebuffer visible on your screen, simply pass 0.

glBindFramebuffer(GL_FRAMEBUFFER, 0);

Note that although only the default framebuffer will be visible on your screen, you can read any framebuffer that is currently bound with a call to glReadPixels as long as it's not only bound to GL_DRAW_FRAMEBUFFER.

Post-processing

In games nowadays post-processing effects seem almost just as important as the actual scenes being rendered on screen, and indeed some spectacular results can be accomplished with different techniques. Post-processing effects in real-time graphics are commonly implemented in fragment shaders with the rendered scene as input in the form of a texture. Framebuffer objects allow us to use a texture to contain the color buffer, so we can use them to prepare input for a post-processing effect.

To use shaders to create a post-processing effect for a scene previously rendered to a texture, it is commonly rendered as a screen filling 2D rectangle. That way the original scene with the effect applied fills the screen at its original size as if it was rendered to the default framebuffer in the first place.

Of course you can get creative with framebuffers and use them to do anything from portals to cameras in the game world by rendering a scene multiple times from different angles and display that on monitors or other objects in the final image. These uses are more specific, so I'll leave them as an exercise to you.

Changing the code

Unfortunately it's a bit more difficult to cover the changes to the code step-by-step here, especially if you've strayed from the sample code here. Now that you know how a framebuffer is created and bound however and with some care put into it, you should be able to do it. Let's globally walk through the steps here.

• First try creating the framebuffer and checking if it is complete. Try binding it as render target and you'll see that your screen turns black because the scene is no longer rendered to the default framebuffer. Try changing the clear color of the scene and reading it back using glReadPixels to check if the scene renders properly to the new framebuffer.
• Next, try creating a new shader program, vertex array object and vertex buffer object to render things in 2D as opposed to 3D. It is useful to switch back to the default framebuffer for this to easily see your results. Your 2D shader shouldn't need transformation matrices. Try rendering a rectangle in front of the 3D spinning cube scene this way.
• Finally, try rendering the 3D scene to the framebuffer created by you and the rectangle to the default framebuffer. Now try using the texture of the framebuffer in the rectangle to render the scene.

I've chosen to have only 2 position coordinates and 2 texture coordinates for my 2D rendering. My 2D shaders look like this:

#version 150 core
in vec2 position;
in vec2 texcoord;
out vec2 Texcoord;
void main()
{
    Texcoord = texcoord;
    gl_Position = vec4(position, 0.0, 1.0);
}

#version 150 core
in vec2 Texcoord;
out vec4 outColor;
uniform sampler2D texFramebuffer;
void main()
{
    outColor = texture(texFramebuffer, Texcoord);
}

With this shader, the output of your program should be the same as before you even knew about framebuffers. Rendering a frame roughly looks like this:

// Bind our framebuffer and draw 3D scene (spinning cube)
glBindFramebuffer(GL_FRAMEBUFFER, frameBuffer);
glBindVertexArray(vaoCube);
glEnable(GL_DEPTH_TEST);
glUseProgram(sceneShaderProgram);

glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, texKitten);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, texPuppy);

// Draw cube scene here

// Bind default framebuffer and draw contents of our framebuffer
glBindFramebuffer(GL_FRAMEBUFFER, 0);
glBindVertexArray(vaoQuad);
glDisable(GL_DEPTH_TEST);
glUseProgram(screenShaderProgram);

glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, texColorBuffer);

glDrawArrays(GL_TRIANGLES, 0, 6);

The 3D and 2D drawing operations both have their own vertex array (cube versus quad), shader program (3D vs 2D post-processing) and textures. You can see that binding the color buffer texture is just as easy as binding regular textures. Do mind that calls like glBindTexture which change the OpenGL state are relatively expensive, so try keeping them to a minimum.

I think that no matter how well I explain the general structure of the program here, some of you just like to look at some new sample code and perhaps run a diff on it and the code from the previous chapter.

Post-processing effects

I will now discuss various interesting post-processing effects, how they work and what they look like.

Color manipulation

Inverting the colors is an option usually found in image manipulation programs, but you can also do it yourself using shaders!

As color values are floating point values ranging from 0.0 to 1.0, inverting a channel is as simple as calculating 1.0 - channel. If you do this for each channel (red, green, blue) you'll get an inverted color. In the fragment shader, that can be done like this.

outColor = vec4(1.0, 1.0, 1.0, 1.0) - texture(texFramebuffer, Texcoord);

This will also affect the alpha channel, but that doesn't matter because alpha blending is disabled by default.

Making colors grayscale can be naively done by calculating the average intensity of each channel.

outColor = texture(texFramebuffer, Texcoord);
float avg = (outColor.r + outColor.g + outColor.b) / 3.0;
outColor = vec4(avg, avg, avg, 1.0);

This works fine, but humans are the most sensitive to green and the least to blue, so a better conversion would work with weighed channels.

outColor = texture(texFramebuffer, Texcoord);
float avg = 0.2126 * outColor.r + 0.7152 * outColor.g + 0.0722 * outColor.b;
outColor = vec4(avg, avg, avg, 1.0);

Blur

There are two well known blur techniques: box blur and Gaussian blur. The latter results in a higher quality result, but the former is easier to implement and still approximates Gaussian blur fairly well.

Blurring is done by sampling pixels around a pixel and calculating the average color.

const float blurSizeH = 1.0 / 300.0;
const float blurSizeV = 1.0 / 200.0;
void main()
{
    vec4 sum = vec4(0.0);
    for (int x = -4; x <= 4; x++)
    	for (int y = -4; y <= 4; y++)
    		sum += texture(
    			texFramebuffer,
    			vec2(Texcoord.x + x * blurSizeH, Texcoord.y + y * blurSizeV)
    		) / 81.0;
    outColor = sum;
}

You can see that a total amount of 81 samples is taken. You can change the amount of samples on the X and Y axes to control the amount of blur. The blurSize variables are used to determine the distance between each sample. A higher sample count and lower sample distance results in a better approximation, but also rapidly decreases performance, so try finding a good balance.

Sobel

The Sobel operator is often used in edge detection algorithms, let's find out what it looks like.

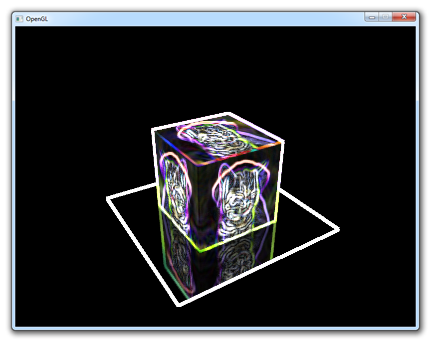
The fragment shader looks like this:

vec4 top         = texture(texFramebuffer, vec2(Texcoord.x, Texcoord.y + 1.0 / 200.0));
vec4 bottom      = texture(texFramebuffer, vec2(Texcoord.x, Texcoord.y - 1.0 / 200.0));
vec4 left        = texture(texFramebuffer, vec2(Texcoord.x - 1.0 / 300.0, Texcoord.y));
vec4 right       = texture(texFramebuffer, vec2(Texcoord.x + 1.0 / 300.0, Texcoord.y));
vec4 topLeft     = texture(texFramebuffer, vec2(Texcoord.x - 1.0 / 300.0, Texcoord.y + 1.0 / 200.0));
vec4 topRight    = texture(texFramebuffer, vec2(Texcoord.x + 1.0 / 300.0, Texcoord.y + 1.0 / 200.0));
vec4 bottomLeft  = texture(texFramebuffer, vec2(Texcoord.x - 1.0 / 300.0, Texcoord.y - 1.0 / 200.0));
vec4 bottomRight = texture(texFramebuffer, vec2(Texcoord.x + 1.0 / 300.0, Texcoord.y - 1.0 / 200.0));
vec4 sx = -topLeft - 2 * left - bottomLeft + topRight   + 2 * right  + bottomRight;
vec4 sy = -topLeft - 2 * top  - topRight   + bottomLeft + 2 * bottom + bottomRight;
vec4 sobel = sqrt(sx * sx + sy * sy);
outColor = sobel;

Just like the blur shader, a few samples are taken and combined in an interesting way. You can read more about the technical details elsewhere.

Conclusion

The cool thing about shaders is that you can manipulate images on a per-pixel basis in real time because of the immense parallel processing capabilities of your graphics card. It is no surprise that newer versions of software like Photoshop use the graphics card to accelerate image manipulation operations! There are many more complex effects like HDR, motion blur and SSAO (screen space ambient occlusion), but those involve a little more work than a single shader, so they're beyond the scope of this chapter.

Exercises

• Try implementing the two-pass Gaussian blur effect by adding another framebuffer. (Solution)
• Try adding a panel in the 3D scene displaying that very scene from a different angle. (Solution)

Geometry shaders

So far we've used vertex and fragment shaders to manipulate our input vertices into pixels on the screen. Since OpenGL 3.2 there is a third optional type of shader that sits between the vertex and fragment shaders, known as the geometry shader. This shader has the unique ability to create new geometry on the fly using the output of the vertex shader as input.

Since we've neglected the kitten from the previous chapters for too long, it ran off to a new home. This gives us a good opportunity to start fresh. At the end of this chapter, we'll have the following demo:

That doesn't look all that exciting... until you consider that the result above was produced with a single draw call:

glDrawArrays(GL_POINTS, 0, 4);

Note that everything geometry shaders can do can be accomplished in other ways, but their ability to generate geometry from a small amount of input data allows you to reduce CPU -> GPU bandwidth usage.

Setup

Let's start by writing some simple code that just draws 4 red points to the screen.

// Vertex shader
const char* vertexShaderSrc = R"glsl(
    #version 150 core
    in vec2 pos;

    void main()
    {
        gl_Position = vec4(pos, 0.0, 1.0);
    }
)glsl";

// Fragment shader
const char* fragmentShaderSrc = R"glsl(
    #version 150 core
    out vec4 outColor;

    void main()
    {
        outColor = vec4(1.0, 0.0, 0.0, 1.0);
    }
)glsl";

We'll start by declaring two very simple vertex and fragment shaders at the top of the file. The vertex shader simply forwards the position attribute of each point and the fragment shader always outputs red. Nothing special there.

Let's also add a helper function to create and compile a shader:

GLuint createShader(GLenum type, const GLchar* src) {
    GLuint shader = glCreateShader(type);
    glShaderSource(shader, 1, &src, nullptr);
    glCompileShader(shader);
    return shader;
}

In the main function, create a window and OpenGL context with a library of choice and initialize GLEW. The shaders and compiled and activated:

GLuint vertexShader = createShader(GL_VERTEX_SHADER, vertexShaderSrc);
GLuint fragmentShader = createShader(GL_FRAGMENT_SHADER, fragmentShaderSrc);

GLuint shaderProgram = glCreateProgram();
glAttachShader(shaderProgram, vertexShader);
glAttachShader(shaderProgram, fragmentShader);
glLinkProgram(shaderProgram);
glUseProgram(shaderProgram);

After that, create a buffer that holds the coordinates of the points:

GLuint vbo;
glGenBuffers(1, &vbo);

float points[] = {
    -0.45f,  0.45f,
     0.45f,  0.45f,
     0.45f, -0.45f,
    -0.45f, -0.45f,
};

glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(points), points, GL_STATIC_DRAW);

We have 4 points here, each with x and y device coordinates. Remember that device coordinates range from -1 to 1 from left to right and bottom to top of the screen, so each corner will have a point.

Then create a VAO and set the vertex format specification:

// Create VAO
GLuint vao;
glGenVertexArrays(1, &vao);
glBindVertexArray(vao);

// Specify layout of point data
GLint posAttrib = glGetAttribLocation(shaderProgram, "pos");
glEnableVertexAttribArray(posAttrib);
glVertexAttribPointer(posAttrib, 2, GL_FLOAT, GL_FALSE, 0, 0);

And finally the render loop:

glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
glClear(GL_COLOR_BUFFER_BIT);

glDrawArrays(GL_POINTS, 0, 4);

With this code, you should now see 4 red points on a black background as shown below:

If you are having problems, have a look at the reference source code.

Basic geometry shader

To understand how a geometry shader works, let's look at an example:

#version 150 core

layout(points) in;
layout(line_strip, max_vertices = 2) out;

void main()
{
    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    EndPrimitive();
}

Input types

Whereas a vertex shader processes vertices and a fragment shader processes fragments, a geometry shader processes entire primitives. The first line describes what kind of primitives our shader should process.

layout(points) in;

The available types are listed below, along with their equivalent drawing command types:

• points - GL_POINTS (1 vertex)
• lines - GL_LINES, GL_LINE_STRIP, GL_LINE_LIST (2 vertices)
• lines_adjacency - GL_LINES_ADJACENCY, GL_LINE_STRIP_ADJACENCY (4 vertices)
• triangles - GL_TRIANGLES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN (3 vertices)
• triangles_adjacency - GL_TRIANGLES_ADJACENCY, GL_TRIANGLE_STRIP_ADJACENCY (6 vertices)

Since we're drawing GL_POINTS, the points type is appropriate.

Output types

The next line describes the output of the shader. What's interesting about geometry shaders is that they can output an entirely different type of geometry and the number of generated primitives can even vary!

layout(line_strip, max_vertices = 2) out;

The second line specifies the output type and the maximum amount of vertices it can pass on. This is the maximum amount for the shader invocation, not for a single primitive (line_strip in this case).

The following output types are available:

• points
• line_strip
• triangle_strip

These types seem somewhat restricted, but if you think about it, these types are sufficient to cover all possible types of primitives. For example, a triangle_strip with only 3 vertices is equivalent to a regular triangle.

Vertex input

The gl_Position, as set in the vertex shader, can be accessed using the gl_in array in the geometry shader. It is an array of structs that looks like this:

in gl_PerVertex
{
    vec4 gl_Position;
    float gl_PointSize;
    float gl_ClipDistance[];
} gl_in[];

Notice that vertex attributes like pos and color are not included, we'll look into accessing those later.

Vertex output

The geometry shader program can call two special functions to generate primitives, EmitVertex and EndPrimitive. Each time the program calls EmitVertex, a vertex is added to the current primitive. When all vertices have been added, the program calls EndPrimitive to generate the primitive.

void main()
{
    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    EndPrimitive();
}

Before calling EmitVertex, the attributes of the vertex should be assigned to variables like gl_Position, just like in the vertex shader. We'll look at setting attributes like color for the fragment shader later.

Now that you know the meaning of every line, can you explain what this geometric shader does?

It creates a single horizontal line for each point coordinate passed to it.

Creating a geometry shader

There's not much to explain, geometry shaders are created and activated in exactly the same way as other types of shaders. Let's add a geometry shader to our 4 point sample that doesn't do anything yet.

const char* geometryShaderSrc = R"glsl(
    #version 150 core

    layout(points) in;
    layout(points, max_vertices = 1) out;

    void main()
    {
        gl_Position = gl_in[0].gl_Position;
        EmitVertex();
        EndPrimitive();
    }
)glsl";

This geometry shader should be fairly straightforward. For each input point, it generates one equivalent output point. This is the minimum amount of code necessary to still display the points on the screen.

With the helper function, creating a geometry shader is easy:

GLuint geometryShader = createShader(GL_GEOMETRY_SHADER, geometryShaderSrc);

There's nothing special about attaching it to the shader program either:

glAttachShader(shaderProgram, geometryShader);

When you run the program now, it should still display the points as before. You can verify that the geometry shader is now doing its work by removing the code from its main function. You'll see that no points are being drawn anymore, because none are being generated!

Now, try replacing the geometry shader code with the line strip generating code from the previous section:

#version 150 core

layout(points) in;
layout(line_strip, max_vertices = 2) out;

void main()
{
    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.0, 0.0, 0.0);
    EmitVertex();

    EndPrimitive();
}

Even though we've made no changes to our draw call, the GPU is suddenly drawing tiny lines instead of points!

Try experimenting a bit to get a feel for it. For example, try outputting rectangles by using triangle_strip.

Geometry shaders and vertex attributes

Let's add some variation to the lines that are being drawn by allowing each of them to have a unique color. By adding a color input variable to the vertex shader, we can specify a color per vertex and thus per generated line.

#version 150 core

in vec2 pos;
in vec3 color;

out vec3 vColor; // Output to geometry (or fragment) shader

void main()
{
    gl_Position = vec4(pos, 0.0, 1.0);
    vColor = color;
}

Update the vertex specification in the program code:

GLint posAttrib = glGetAttribLocation(shaderProgram, "pos");
glEnableVertexAttribArray(posAttrib);
glVertexAttribPointer(posAttrib, 2, GL_FLOAT, GL_FALSE, 5 * sizeof(float), 0);

GLint colAttrib = glGetAttribLocation(shaderProgram, "color");
glEnableVertexAttribArray(colAttrib);
glVertexAttribPointer(colAttrib, 3, GL_FLOAT, GL_FALSE,
                       5 * sizeof(float), (void*) (2 * sizeof(float)));

And update the point data to include an RGB color per point:

float points[] = {
    -0.45f,  0.45f, 1.0f, 0.0f, 0.0f, // Red point
     0.45f,  0.45f, 0.0f, 1.0f, 0.0f, // Green point
     0.45f, -0.45f, 0.0f, 0.0f, 1.0f, // Blue point
    -0.45f, -0.45f, 1.0f, 1.0f, 0.0f, // Yellow point
};

Because the vertex shader is now not followed by a fragment shader, but a geometry shader, we have to handle the vColor variable as input there.

#version 150 core

layout(points) in;
layout(line_strip, max_vertices = 2) out;

in vec3 vColor[]; // Output from vertex shader for each vertex

out vec3 fColor; // Output to fragment shader

void main()
{
    ...

You can see that it is very similar to how inputs are handled in the fragment shader. The only difference is that inputs must be arrays now, because the geometry shader can receive primitives with multiple vertices as input, each with its own attribute values.

Because the color needs to be passed further down to the fragment shader, we add it as output of the geometry shader. We can now assign values to it, just like we did earlier with gl_Position.

void main()
{
    fColor = vColor[0]; // Point has only one vertex

    gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.1, 0.0, 0.0);
    EmitVertex();

    gl_Position = gl_in[0].gl_Position + vec4(0.1, 0.1, 0.0, 0.0);
    EmitVertex();

    EndPrimitive();
}

Whenever EmitVertex is called now, a vertex is emitted with the current value of fColor as color attribute. We can now access that attribute in the fragment shader:

#version 150 core

in vec3 fColor;

out vec4 outColor;

void main()
{
    outColor = vec4(fColor, 1.0);
}

So, when you specify an attribute for a vertex, it is first passed to the vertex shader as input. The vertex shader can then choose to output it to the geometry shader. And then the geometry shader can choose to further output it to the fragment shader.

However, this demo is not very interesting. We could easily replicate this behaviour by creating a vertex buffer with a single line and issuing a couple of draw calls with different colors and positions set with uniform variables.

Dynamically generating geometry

The real power of geometry shader lies in the ability to generate a varying amount of primitives, so let's create a demo that properly abuses this ability.

Let's say you're making a game where the world consists of circles. You could draw a single model of a circle and repeatedly draw it, but this approach is not ideal. If you're too close, these "circles" will look like ugly polygons and if you're too far away, your graphics card is wasting performance on rendering complexity you can't even see.

We can do better with geometry shaders! We can write a shader that generates the appropriate resolution circle based on run-time conditions. Let's first modify the geometry shader to draw a 10-sided polygon at each point. If you remember your trigonometry, it should be a piece of cake:

#version 150 core

layout(points) in;
layout(line_strip, max_vertices = 11) out;

in vec3 vColor[];
out vec3 fColor;

const float PI = 3.1415926;

void main()
{
    fColor = vColor[0];

    for (int i = 0; i <= 10; i++) {
        // Angle between each side in radians
        float ang = PI * 2.0 / 10.0 * i;

        // Offset from center of point (0.3 to accomodate for aspect ratio)
        vec4 offset = vec4(cos(ang) * 0.3, -sin(ang) * 0.4, 0.0, 0.0);
        gl_Position = gl_in[0].gl_Position + offset;

        EmitVertex();
    }

    EndPrimitive();
}

The first point is repeated to close the line loop, which is why 11 vertices are drawn. The result is as expected:

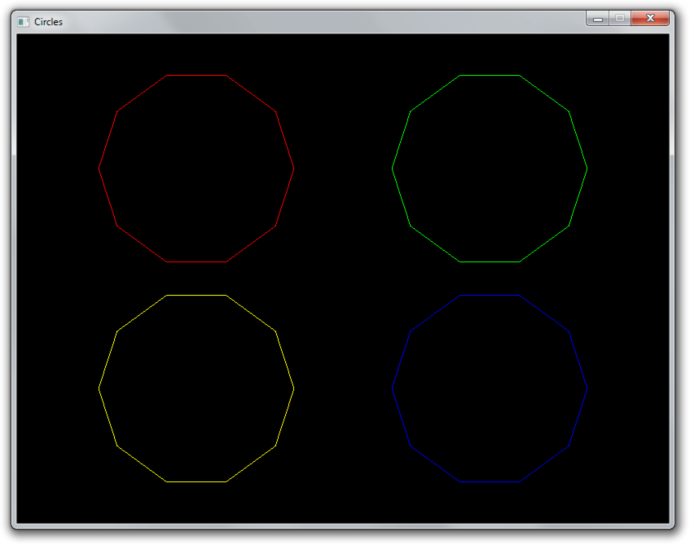
It is now trivial to add a vertex attribute to control the amount of sides. Add the new attribute to the data and to the specification:

float points[] = {
//  Coordinates  Color             Sides
    -0.45f,  0.45f, 1.0f, 0.0f, 0.0f,  4.0f,
     0.45f,  0.45f, 0.0f, 1.0f, 0.0f,  8.0f,
     0.45f, -0.45f, 0.0f, 0.0f, 1.0f, 16.0f,
    -0.45f, -0.45f, 1.0f, 1.0f, 0.0f, 32.0f
};

...

// Specify layout of point data
GLint posAttrib = glGetAttribLocation(shaderProgram, "pos");
glEnableVertexAttribArray(posAttrib);
glVertexAttribPointer(posAttrib, 2, GL_FLOAT, GL_FALSE,
                       6 * sizeof(float), 0);

GLint colAttrib = glGetAttribLocation(shaderProgram, "color");
glEnableVertexAttribArray(colAttrib);
glVertexAttribPointer(colAttrib, 3, GL_FLOAT, GL_FALSE,
                       6 * sizeof(float), (void*) (2 * sizeof(float)));

GLint sidesAttrib = glGetAttribLocation(shaderProgram, "sides");
glEnableVertexAttribArray(sidesAttrib);
glVertexAttribPointer(sidesAttrib, 1, GL_FLOAT, GL_FALSE,
                       6 * sizeof(float), (void*) (5 * sizeof(float)));

Alter the vertex shader to pass the value to the geometry shader:

#version 150 core

in vec2 pos;
in vec3 color;
in float sides;

out vec3 vColor;
out float vSides;

void main()
{
    gl_Position = vec4(pos, 0.0, 1.0);
    vColor = color;
    vSides = sides;
}

And use the variable in the geometry shader instead of the magic number of sides 10.0. It's also necessary to set an appropriate max_vertices value for our input, otherwise the circles with more vertices will be cut off.

layout(line_strip, max_vertices = 64) out;

...

in float vSides[];

...

// Safe, floats can represent small integers exactly
for (int i = 0; i <= vSides[0]; i++) {
    // Angle between each side in radians
    float ang = PI * 2.0 / vSides[0] * i;

    ...

You can now create a circles with any amount of sides you desire by simply adding more points!

Without a geometry shader, we'd have to rebuild the entire vertex buffer whenever any of these circles have to change, now we can simply change the value of a vertex attribute. In a game setting, this attribute could be changed based on player distance as described above. You can find the full code here.

Conclusion

Granted, geometry shaders may not have as many real world use cases as things like framebuffers and textures have, but they can definitely help with creating content on the GPU as shown here.

If you need to repeat a single mesh many times, like a cube in a voxel game, you could create a geometry shader that generates cubes from points in a similar fashion. However, for these cases where each generated mesh is exactly the same, there are more efficient methods like instancing.

Lastly, with regards to portability, the latest WebGL and OpenGL ES standards do not yet support geometry shaders, so keep that in mind if you're considering the development of a mobile or web application.

Exercises

• Try using a geometry shader in a 3D scenario to create more complex meshes like cubes from points. (Solution)

Transform feedback

Up until now we've always sent vertex data to the graphics processor and only produced drawn pixels in framebuffers in return. What if we want to retrieve the vertices after they've passed through the vertex or geometry shaders? In this chapter we'll look at a way to do this, known as transform feedback.

So far, we've used VBOs (Vertex Buffer Objects) to store vertices to be used for drawing operations. The transform feedback extension allows shaders to write vertices back to these as well. You could for example build a vertex shader that simulates gravity and writes updated vertex positions back to the buffer. This way you don't have to transfer this data back and forth from graphics memory to main memory. On top of that, you get to benefit from the vast parallel processing power of today's GPUs.

Basic feedback

We'll start from scratch so that the final program will clearly demonstrate how simple transform feedback is. Unfortunately there's no preview this time, because we're not going to draw anything in this chapter! Although this feature can be used to simplify effects like particle simulation, explaining these is a bit beyond the scope of these articles. After you've understood the basics of transform feedback, you'll be able to find and understand plenty of articles around the web on these topics.

Let's start with a simple vertex shader.

const GLchar* vertexShaderSrc = R"glsl(
    in float inValue;
    out float outValue;

    void main()
    {
        outValue = sqrt(inValue);
    }
)glsl";

This vertex shader does not appear to make much sense. It doesn't set a gl_Position and it only takes a single arbitrary float as input. Luckily, we can use transform feedback to capture the result, as we'll see momentarily.

GLuint shader = glCreateShader(GL_VERTEX_SHADER);
glShaderSource(shader, 1, &vertexShaderSrc, nullptr);
glCompileShader(shader);

GLuint program = glCreateProgram();
glAttachShader(program, shader);

Compile the shader, create a program and attach the shader, but don't call glLinkProgram yet! Before linking the program, we have to tell OpenGL which output attributes we want to capture into a buffer.

const GLchar* feedbackVaryings[] = { "outValue" };
glTransformFeedbackVaryings(program, 1, feedbackVaryings, GL_INTERLEAVED_ATTRIBS);

The first parameter is self-explanatory, the second and third parameter specify the length of the output names array and the array itself, and the final parameter specifies how the data should be written.

The following two formats are available:

• GL_INTERLEAVED_ATTRIBS: Write all attributes to a single buffer object.
• GL_SEPARATE_ATTRIBS: Writes attributes to multiple buffer objects or at different offsets into a buffer.

Sometimes it is useful to have separate buffers for each attribute, but lets keep it simple for this demo. Now that you've specified the output variables, you can link and activate the program. That is because the linking process depends on knowledge about the outputs.

glLinkProgram(program);
glUseProgram(program);

After that, create and bind the VAO:

GLuint vao;
glGenVertexArrays(1, &vao);
glBindVertexArray(vao);

Now, create a buffer with some input data for the vertex shader:

GLfloat data[] = { 1.0f, 2.0f, 3.0f, 4.0f, 5.0f };

GLuint vbo;
glGenBuffers(1, &vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(data), data, GL_STATIC_DRAW);

The numbers in data are the numbers we want the shader to calculate the square root of and transform feedback will help us get the results back.

With regards to vertex pointers, you know the drill by now:

GLint inputAttrib = glGetAttribLocation(program, "inValue");
glEnableVertexAttribArray(inputAttrib);
glVertexAttribPointer(inputAttrib, 1, GL_FLOAT, GL_FALSE, 0, 0);

Transform feedback will return the values of outValue, but first we'll need to create a VBO to hold these, just like the input vertices:

GLuint tbo;
glGenBuffers(1, &tbo);
glBindBuffer(GL_ARRAY_BUFFER, tbo);
glBufferData(GL_ARRAY_BUFFER, sizeof(data), nullptr, GL_STATIC_READ);

Notice that we now pass a nullptr to create a buffer big enough to hold all of the resulting floats, but without specifying any initial data. The appropriate usage type is now GL_STATIC_READ, which indicates that we intend OpenGL to write to this buffer and our application to read from it. (See reference for usage types)

We've now made all preparations for the rendering computation process. As we don't intend to draw anything, the rasterizer should be disabled:

glEnable(GL_RASTERIZER_DISCARD);

To actually bind the buffer we've created above as transform feedback buffer, we have to use a new function called glBindBufferBase.

glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 0, tbo);

The first parameter is currently required to be GL_TRANSFORM_FEEDBACK_BUFFER to allow for future extensions. The second parameter is the index of the output variable, which is simply 0 because we only have one. The final parameter specifies the buffer object to bind.

Before doing the draw call, you have to enter transform feedback mode:

glBeginTransformFeedback(GL_POINTS);

It certainly brings back memories of the old glBegin days! Just like the geometry shader in the last chapter, the possible values for the primitive mode are a bit more limited.

• GL_POINTS — GL_POINTS
• GL_LINES — GL_LINES, GL_LINE_LOOP, GL_LINE_STRIP, GL_LINES_ADJACENCY, GL_LINE_STRIP_ADJACENCY
• GL_TRIANGLES — GL_TRIANGLES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES_ADJACENCY, GL_TRIANGLE_STRIP_ADJACENCY

If you only have a vertex shader, as we do now, the primitive must match the one being drawn:

glDrawArrays(GL_POINTS, 0, 5);

Even though we're now working with data, the single numbers can still be seen as separate "points", so we use that primitive mode.

End the transform feedback mode:

glEndTransformFeedback();

Normally, at the end of a drawing operation, we'd swap the buffers to present the result on the screen. We still want to make sure the rendering operation has finished before trying to access the results, so we flush OpenGL's command buffer:

glFlush();

Getting the results back is now as easy as copying the buffer data back to an array:

GLfloat feedback[5];
glGetBufferSubData(GL_TRANSFORM_FEEDBACK_BUFFER, 0, sizeof(feedback), feedback);

If you now print the values in the array, you should see the square roots of the input in your terminal:

printf("%f %f %f %f %f\n", feedback[0], feedback[1], feedback[2], feedback[3], feedback[4]);

Congratulations, you now know how to make your GPU perform general purpose tasks with vertex shaders! Of course a real GPGPU framework like OpenCL is generally better at this, but the advantage of transform feedback is that you can directly repurpose the data in drawing operations, by for example binding the transform feedback buffer as array buffer and performing normal drawing calls.

If you have a graphics card and driver that supports it, you could also use compute shaders in OpenGL 4.3 instead, which were actually designed for tasks that are less related to drawing.

You can find the full code here.

Feedback transform and geometry shaders

When you include a geometry shader, the transform feedback operation will capture the outputs of the geometry shader instead of the vertex shader. For example:

// Vertex shader
const GLchar* vertexShaderSrc = R"glsl(
    in float inValue;
    out float geoValue;

    void main()
    {
        geoValue = sqrt(inValue);
    }
)glsl";

// Geometry shader
const GLchar* geoShaderSrc = R"glsl(
    layout(points) in;
    layout(triangle_strip, max_vertices = 3) out;

    in float[] geoValue;
    out float outValue;

    void main()
    {
        for (int i = 0; i < 3; i++) {
            outValue = geoValue[0] + i;
            EmitVertex();
        }

        EndPrimitive();
    }
)glsl";

The geometry shader takes a point processed by the vertex shader and generates 2 more to form a triangle with each point having a 1 higher value.

GLuint geoShader = glCreateShader(GL_GEOMETRY_SHADER);
glShaderSource(geoShader, 1, &geoShaderSrc, nullptr);
glCompileShader(geoShader);

...

glAttachShader(program, geoShader);

Compile and attach the geometry shader to the program to start using it.

const GLchar* feedbackVaryings[] = { "outValue" };
glTransformFeedbackVaryings(program, 1, feedbackVaryings, GL_INTERLEAVED_ATTRIBS);

Although the output is now coming from the geometry shader, we've not changed the name, so this code remains unchanged.

Because each input vertex will generate 3 vertices as output, the transform feedback buffer now needs to be 3 times as big as the input buffer:

glBufferData(GL_ARRAY_BUFFER, sizeof(data) * 3, nullptr, GL_STATIC_READ);

When using a geometry shader, the primitive specified to glBeginTransformFeedback must match the output type of the geometry shader:

glBeginTransformFeedback(GL_TRIANGLES);

Retrieving the output still works the same:

// Fetch and print results
GLfloat feedback[15];
glGetBufferSubData(GL_TRANSFORM_FEEDBACK_BUFFER, 0, sizeof(feedback), feedback);

for (int i = 0; i < 15; i++) {
    printf("%f\n", feedback[i]);
}

Although you have to pay attention to the feedback primitive type and the size of your buffers, adding a geometry shader to the equation doesn't change much other than the shader responsible for output.

The full code can be found here.

Variable feedback

As we've seen in the previous chapter, geometry shaders have the unique property to generate a variable amount of data. Luckily, there are ways to keep track of how many primitives were written by using query objects.

Just like all the other objects in OpenGL, you'll have to create one first:

GLuint query;
glGenQueries(1, &query);

Then, right before calling glBeginTransformFeedback, you have to tell OpenGL to keep track of the number of primitives written:

glBeginQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN, query);

After glEndTransformFeedback, you can stop "recording":

glEndQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN);

Retrieving the result is done as follows:

GLuint primitives;
glGetQueryObjectuiv(query, GL_QUERY_RESULT, &primitives);

You can then print that value along with the other data:

printf("%u primitives written!\n\n", primitives);

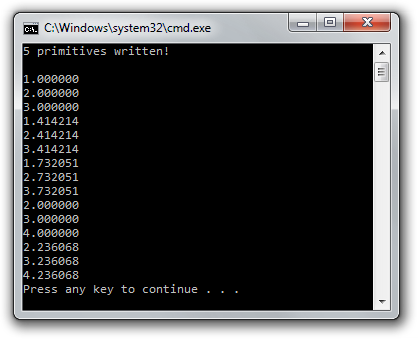
Notice that it returns the number of primitives, not the number of vertices. Since we have 15 vertices, with each triangle having 3, we have 5 primitives.

Query objects can also be used to record things such as GL_PRIMITIVES_GENERATED when dealing with just geometry shaders and GL_TIME_ELAPSED to measure time spent on the server (graphics card) doing work.

See the full code if you got stuck somewhere on the way.

Conclusion

You now know enough about geometry shaders and transform feedback to make your graphics card do some very interesting work besides just drawing! You can even combine transform feedback and rasterization to update vertices and draw them at the same time!

Exercises

• Try writing a vertex shader that simulates gravity to make points hover around the mouse cursor using transform feedback to update the vertices. (Solution)